今回は、「経済学・経済政策」の「無差別曲線」「予算制約線」「最適消費点」「代替効果と所得効果」に関する記事のまとめです。
目次
無差別曲線 -リンク-
本ブログにて「無差別曲線」について説明しているページを以下に示しますのでアクセスしてみてください。
- R3-15 効用理論(6)無差別曲線(右上がりの曲線)
- R2-14 効用理論(1)無差別曲線(完全補完財)
- R1-12 効用理論(2)無差別曲線(限界代替率)
- H29-12 効用理論(3)無差別曲線(垂直の無差別曲線)
- H27-12 効用理論(4)無差別曲線(完全補完財)
- H24-16 効用理論(5)無差別曲線(完全代替材)
予算制約線・最適消費点 -リンク-
本ブログにて「予算制約線」「最適消費点」について説明しているページを以下に示しますのでアクセスしてみてください。
- R3-16 代替効果と所得効果(8)予算制約線・代替効果と所得効果
- R2-13 予算制約と消費者の選択行動(1)予算制約線
- H28-15 予算制約と消費者の選択行動(3)予算制約線と無差別曲線
- H27-14 予算制約と消費者の選択行動(4)効用最大化
- H26-15 予算制約と消費者の選択行動(5)最適消費点
- H25-19 予算制約と消費者の選択行動(6)予算制約線
代替効果と所得効果 -リンク-
本ブログにて「代替効果と所得効果」について説明しているページを以下に示しますのでアクセスしてみてください。
- R3-16 代替効果と所得効果(8)予算制約線・代替効果と所得効果
- R2-15 代替効果と所得効果(1)代替効果と所得効果
- H29-16 代替効果と所得効果(2)代替効果と所得効果
- H28-16 代替効果と所得効果(3)代替効果と所得効果
- H27-13 代替効果と所得効果(4)代替効果と所得効果
- H26-16 代替効果と所得効果(5)代替効果と所得効果
- H25-14 代替効果と所得効果(6)代替効果と所得効果
- H24-17 代替効果と所得効果(7)代替効果と所得効果
効用
消費者は、財を消費することによって「効用」を得ることができます。
「効用」とは「財の消費によって消費者が得られる満足度」のことをいいます。
無差別曲線
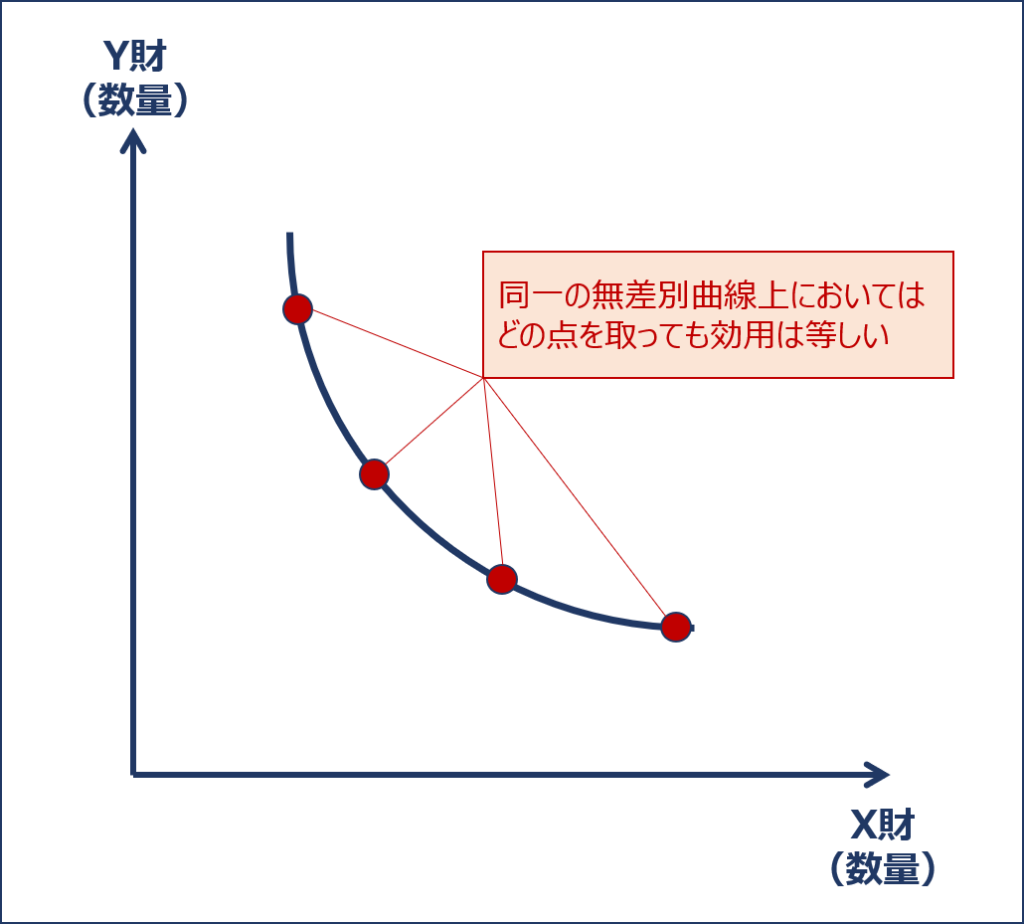
「無差別曲線」とは、社会に2つの財しか存在しないという仮定の「2財モデル」において、縦軸に「Y財の消費量」を、横軸に「X財の消費量」を取ったグラフで表される「ある消費者が等しい効用水準を得られる2財の消費の組み合わせを結んだ曲線」のことをいいます。
消費が増加すると効用が高まる一般的な2つの財の「無差別曲線」は以下の図のようになります。
「無差別曲線」では、「同一の無差別曲線上においてはどの点を取っても効用水準は等しい」という特徴を理解しておくことが重要です。
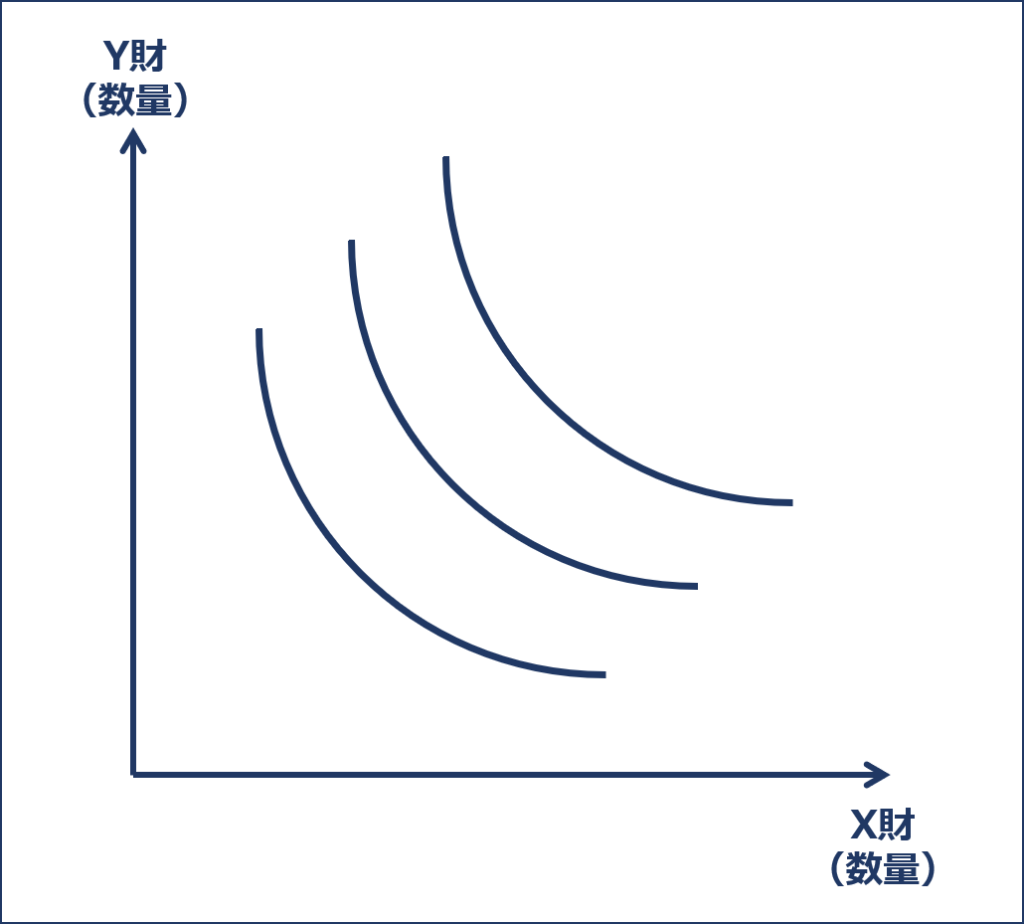
また、もう一つ、「無差別曲線」は以下の図のように「3本」しかないわけではなく無数に存在するという特徴も理解しておくことが重要です。
無差別曲線の特徴
「無差別曲線」に関する4つの特徴を以下に示します。
- 右下がりの曲線となる(単調性の仮定)
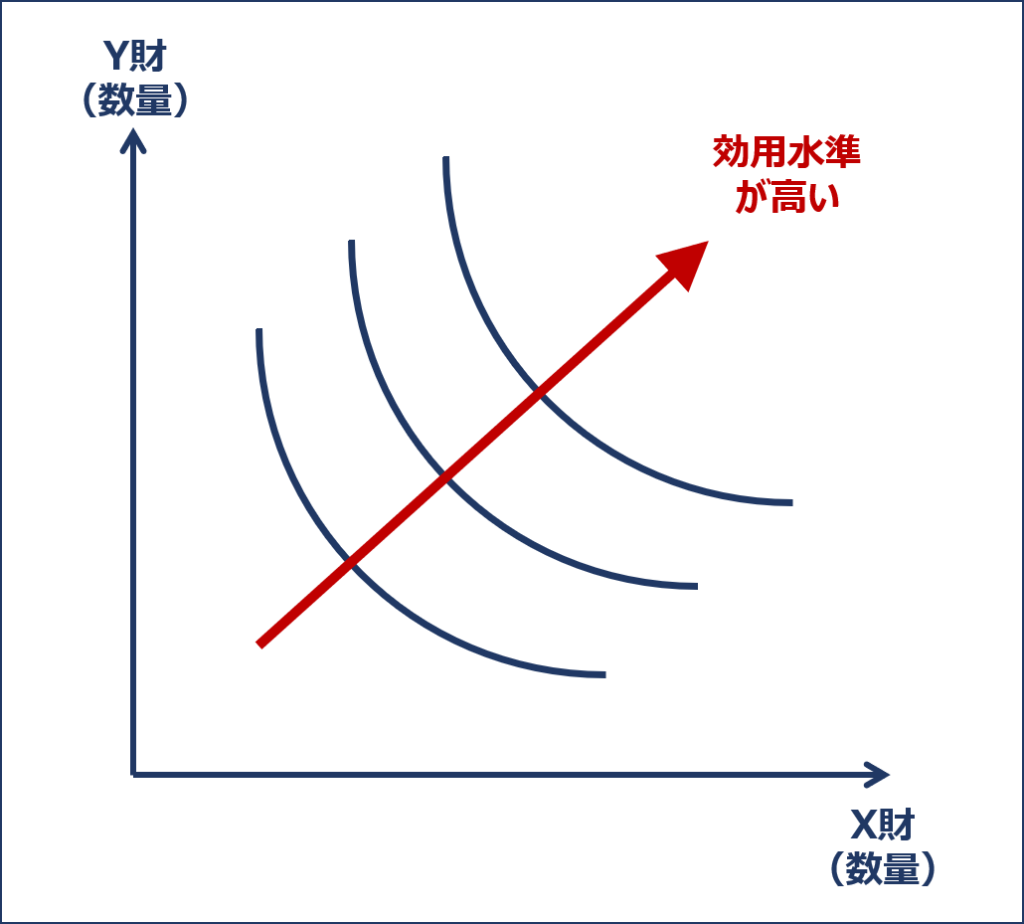
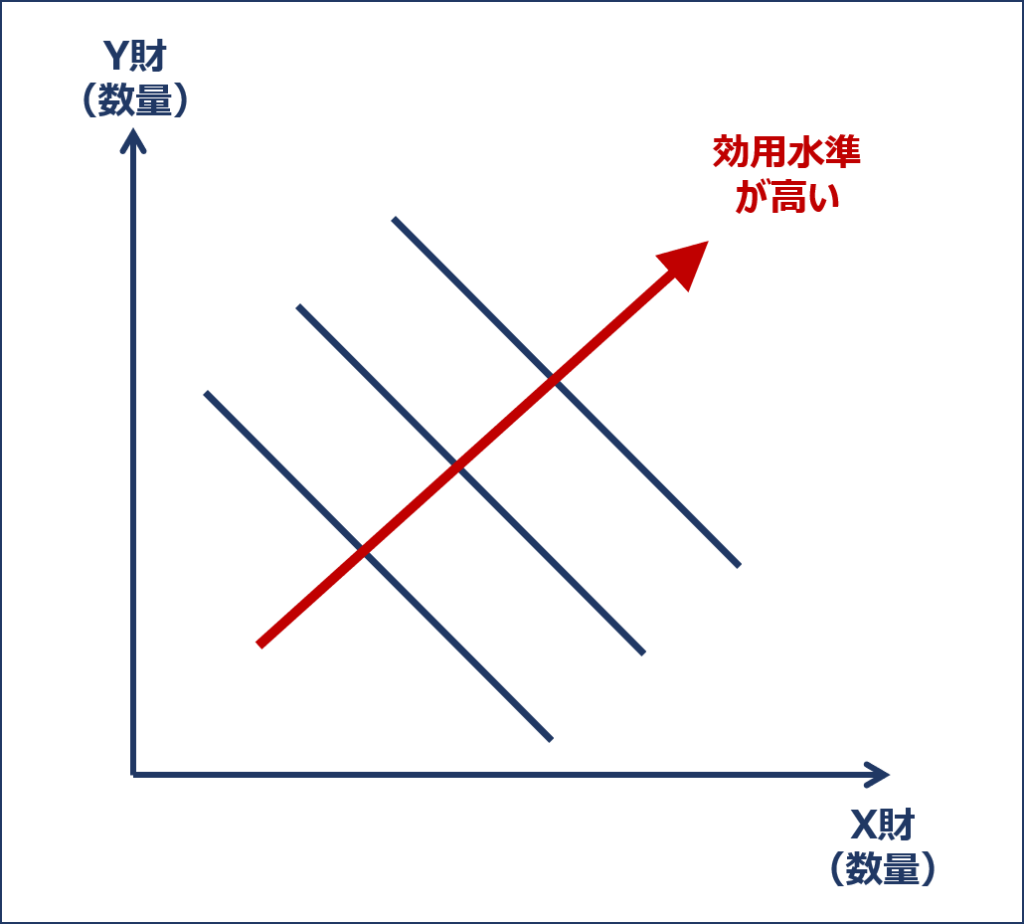
- グラフの右上にある無差別曲線ほど効用水準が高い(非飽和の仮定)
- 効用水準の異なる無差別曲線は互いに交わらない(推移性の仮定)
- 原点に対して凸の曲線となる(限界代替率逓減の法則)
上記の特徴を踏まえ、無差別曲線を描写すると以下の通りとなります。
限界代替率逓減の法則
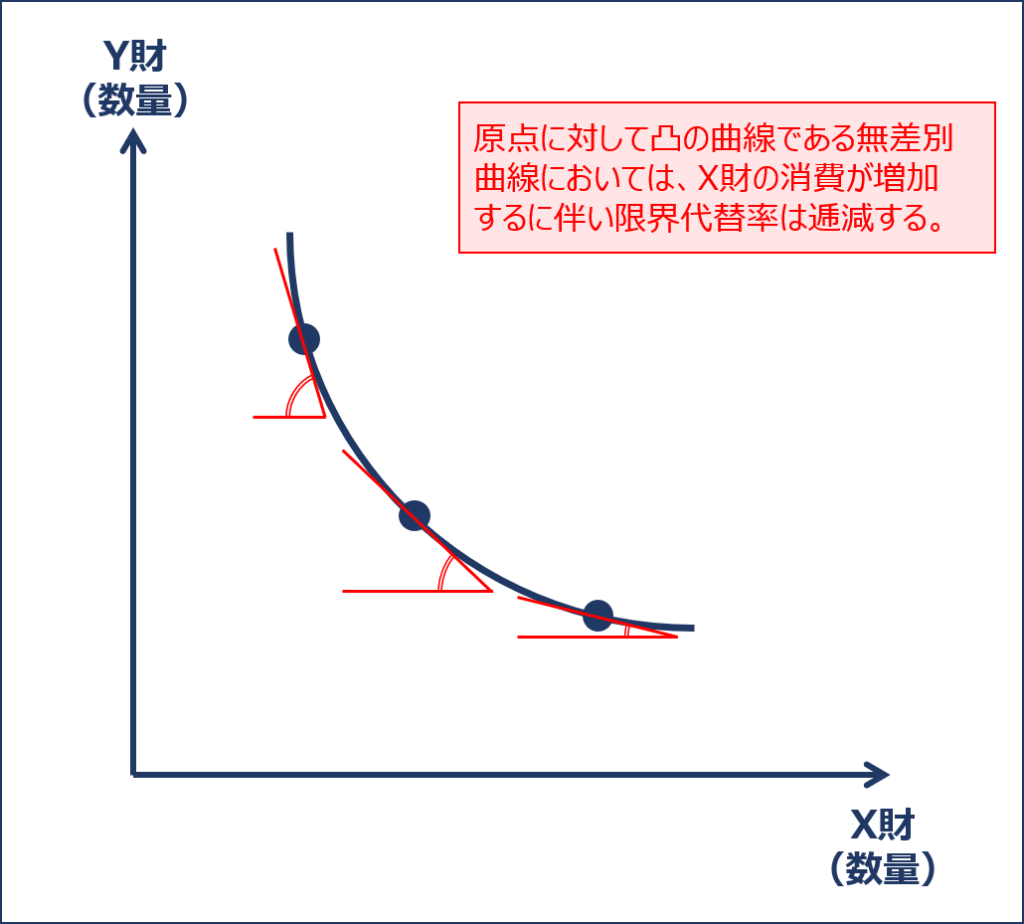
「限界代替率」とは、縦軸に「Y財の消費量」を、横軸に「X財の消費量」を取ったグラフで表される「ある消費者が得られる効用水準が一定という条件において、X財の消費を1単位増加したときのY財の消費の減少分」のことをいい、「無差別曲線」の接線の傾きの絶対値として表されます。
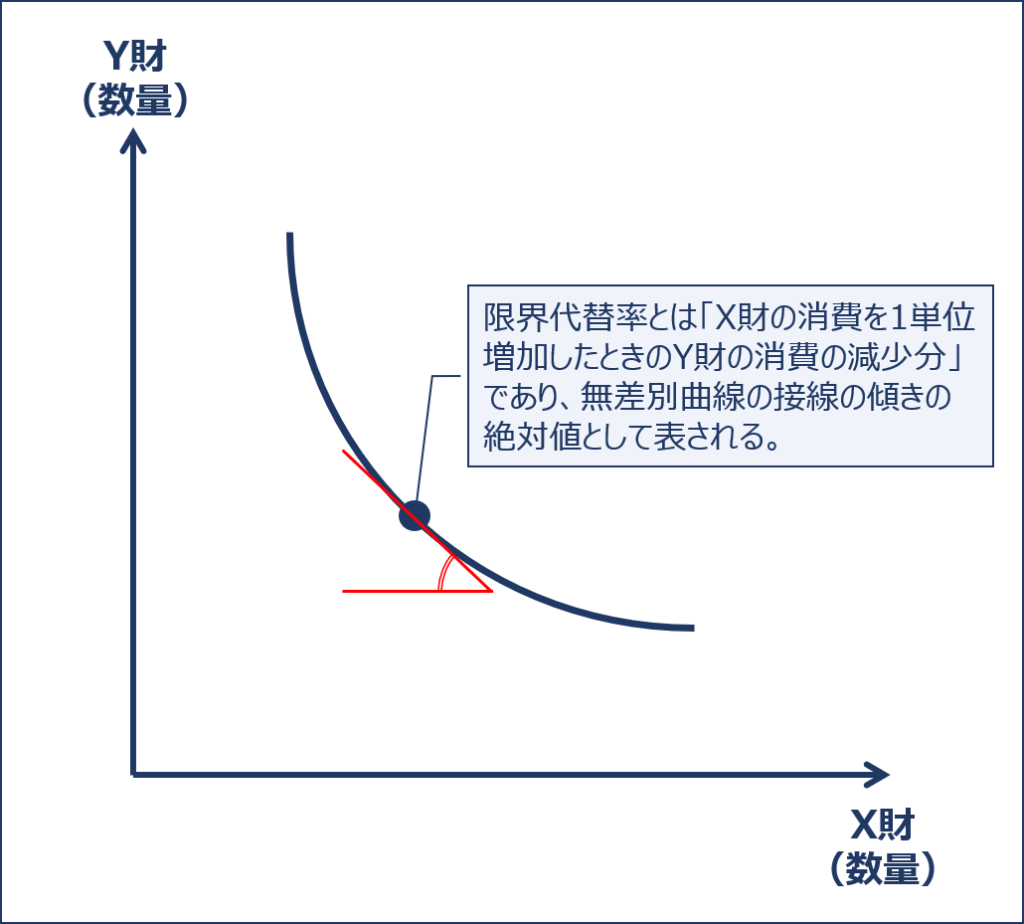
「限界代替率逓減の法則」とは、X財の消費量の増加に伴い「限界代替率」が徐々に減少していく(逓減する)ことをいい、この法則に基づき描画した「無差別曲線」は、原点に対して凸の形状となります。
特殊な形状の無差別曲線
「無差別曲線」は、2つの財の関係により、特殊な形状となるケースがあります。
- 完全代替材(右下がりの直線)
- 完全補完財(L字型)
- 限界代替率逓増(原点に対して凹の曲線)
- 効用が増加する財と効用が減少する財の組み合わせ(右上がりの曲線)
完全代替材(右下がりの直線)
「2財モデル」において、片方の金額が値上がりして需要が減少すると、もう片方の需要が増加するような関係にある財のことを「粗代替財」といいます。
- X財の価格(PX)↑ → X財の需要(X)↓ → Y財の需要(Y)↑
この代替関係が100%である「完全代替財」の「無差別曲線」は「右下がりの直線」となります。
完全補完財(L字型)
「2財モデル」において、片方の金額が値上がりして需要が減少すると、もう片方の需要も減少するような関係にある財のことを「粗補完財」といいます。
- X財の価格(PX)↑ → X財の需要(X)↓ → Y財の需要(Y)↓
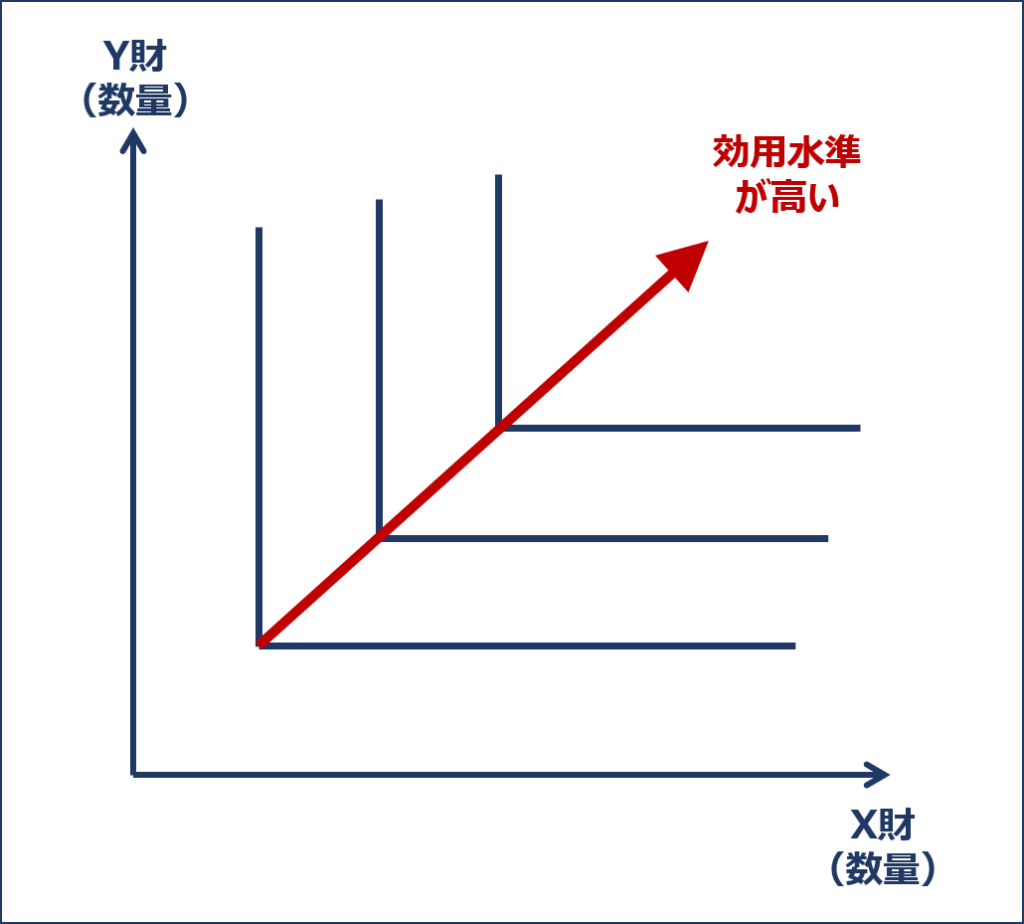
この補完関係が100%である「完全補完財」の「無差別曲線」は「L字型」となります。
「2財を1セットとして消費する財」を例として説明します。
- 左足用の靴と右足用の靴
- ボルトとナット
実際にはそんなことはありませんが、仮に「左足用の靴」と「右足用の靴」が別々に販売されているとした場合の「効用」について考えてみます。
- 「左足用の靴」だけ購入しても使い物にならないため「効用」が得られません。
- 「左足用の靴」を1足購入して「右足用の靴」を1足購入すれば「1セット」の靴として使えるため「効用」が得られます。
- 「左足用の靴」を1足購入して「右足用の靴」を2足購入したとしても、靴としては「1セット」としてしか使えないため「左足用の靴」と「右足用の靴」を「1セット(1足ずつ)」購入したときと同じ「効用」しか得られません。
- 「左足用の靴」を2足購入して「右足用の靴」を2足購入すれば、「2セット」の靴として使えるため「1セット」の靴を購入したときよりも「効用」が高まります。
この「効用」の変化を「無差別曲線」として表すと、以下のように「L字型」となります。
限界代替率逓増(原点に対して凹の曲線)
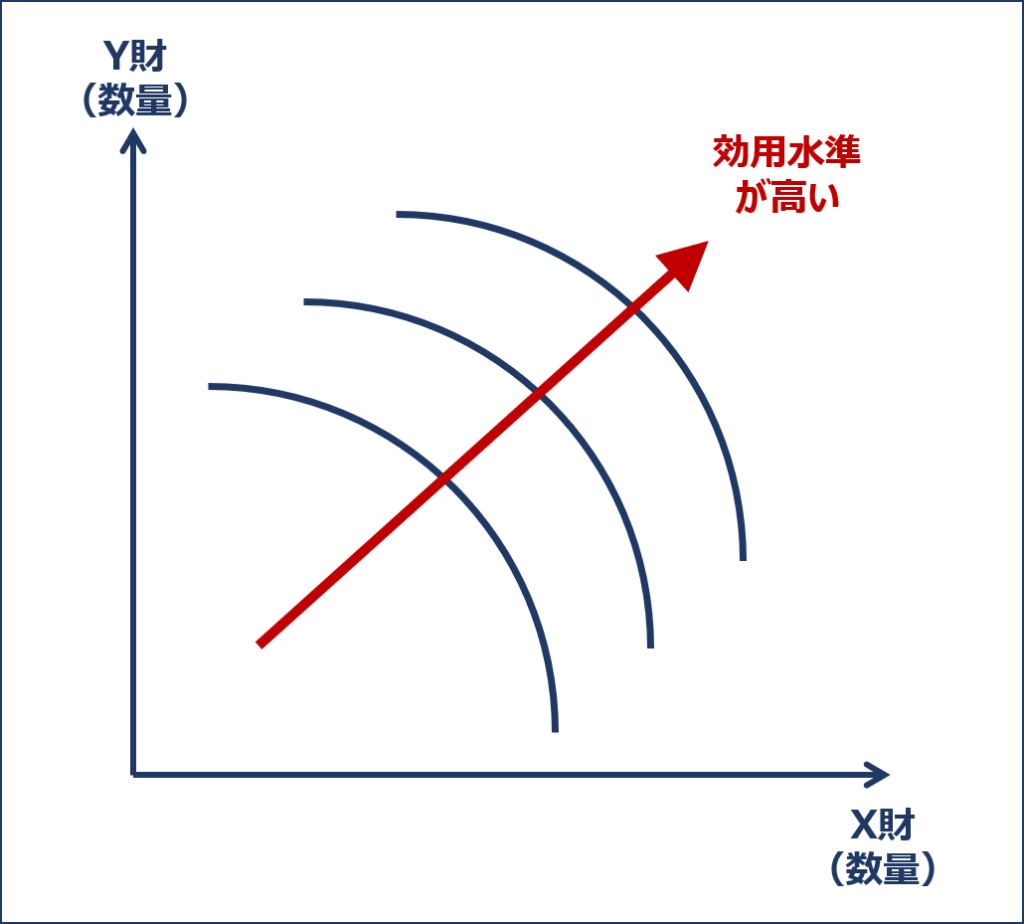
一般的な「無差別曲線」は「限界代替率逓減の法則」に基づいているため、原点に対して凸の曲線となりますが、「限界代替率」が逓増する場合の「無差別曲線」は「原点に対して凹の曲線」となります。
効用が増加する財と効用が減少する財の組み合わせ(右上がりの曲線)
「金融商品」を例として考えてみた場合、一般的に「リスク」の低い金融商品は「リターン」が低く、「リスク」の高い金融商品は「リターン」も高くなっていますが、消費者は「効用」を高めるために、できるだけ「リスク」が低く「リターン」が高い金融商品を探します。
この「リスク」と「リターン」と「効用」の関係を示すと以下の通りです。
- リスクが高く↑+ リターンが低い↓= 効用が低い↓
- リスクが低く↓+ リターンが高い↑= 効用が高い↑
「リターン」を縦軸に「リスク」を横軸に取り、この「効用」の変化を「無差別曲線」として表すと、以下のように「右上がりの曲線」となります。
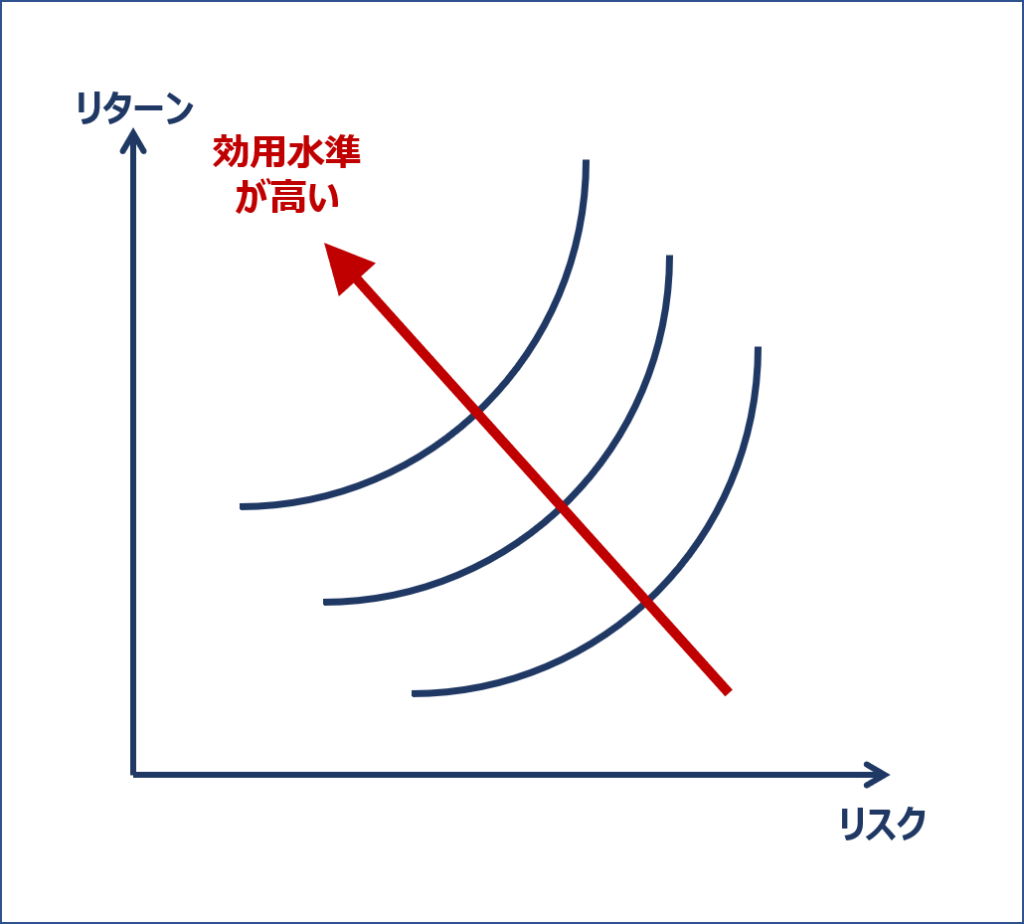
「リターン」を縦軸に「リスク」を横軸に取った「無差別曲線」が、令和元年度の「財務・会計 第13問」で出題されています。
また、「投資の期待収益率」を縦軸に「当該投資収益率の標準偏差」を横軸に取った「無差別曲線」が、平成25年度の「財務・会計 第19問」で出題されています。
予算制約線
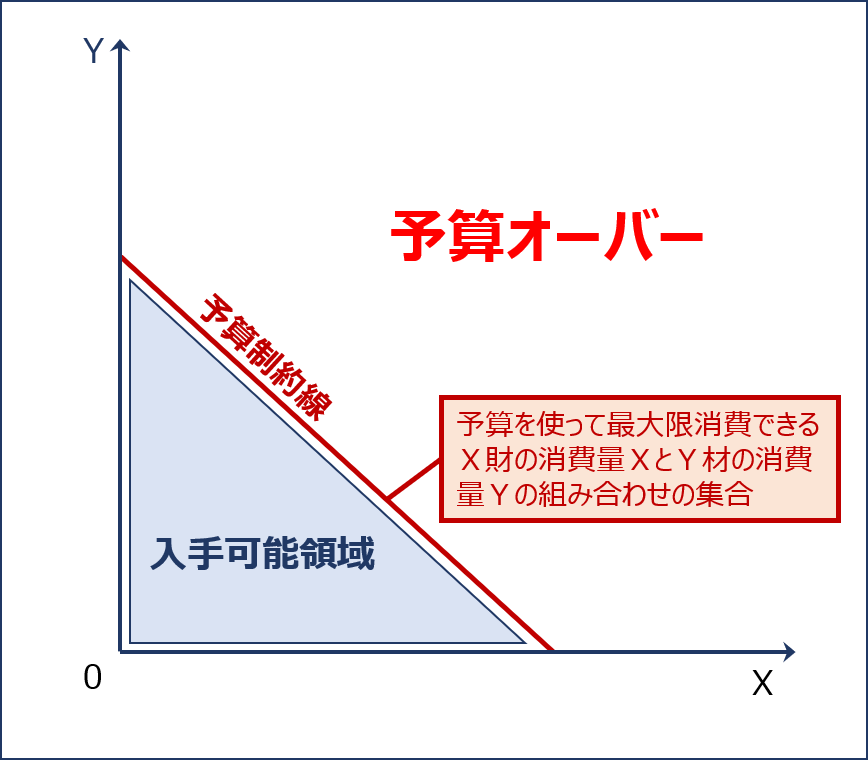
「予算制約線」とは、社会に2つの財しか存在しないという仮定の「2財モデル」において、「X財の消費量X」と「Y財の消費量Y」のグラフで表される「予算を全て使い切った2財の消費の組み合わせを結んだ曲線」のことをいいます。
予算制約線の求め方
「予算制約線」の求め方について説明します。
X財の価格が「PX」であり、Y財の価格が「PY」である場合、X財とY財を消費するときの「総支出」は以下の式により求めることができます。

「予算制約線」とは「予算を全て使い切った2財の消費の組み合わせを結んだ曲線」であるため「予算(M)= 総支出」となる以下の条件式が成立します。

上記の式を「Y=」という形に変形した以下の式が「予算制約線」です。
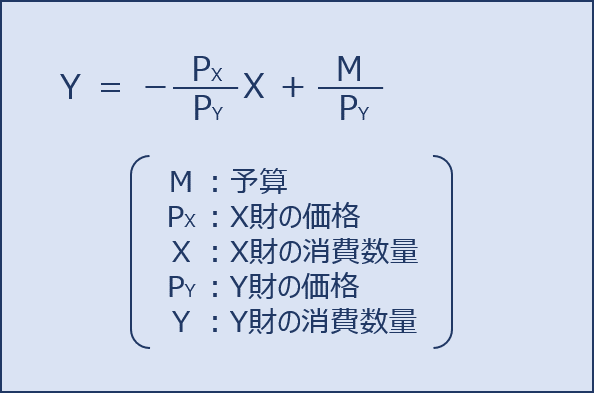
したがって「予算制約線」は以下のように表すことができます。
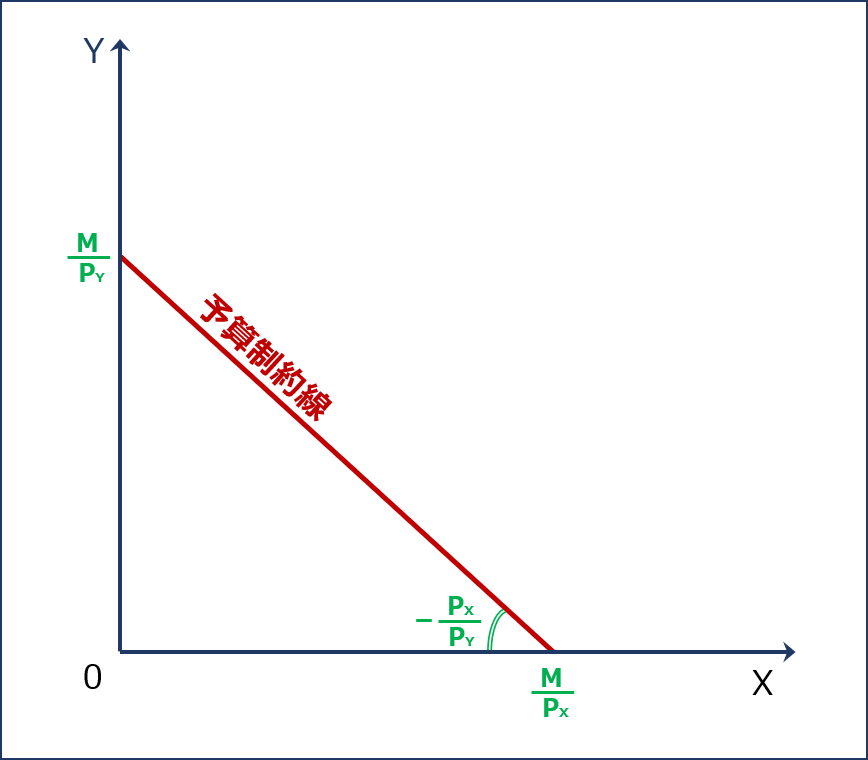
「予算制約線」において、X財とY財を消費するときの「総支出」が予算内に収まっていることを表している「予算制約線」より左下の範囲を「入手可能領域」といいます。なお、「予算制約線」より右上の範囲は「予算オーバー」であることを示しています。

予算制約線のシフト
「予算制約線」は「X財の価格(PX)」「Y財の価格(PY)」「予算(M)」などの条件が変化するとシフトします。
X財の価格が変動する場合
X財の価格が下落する場合
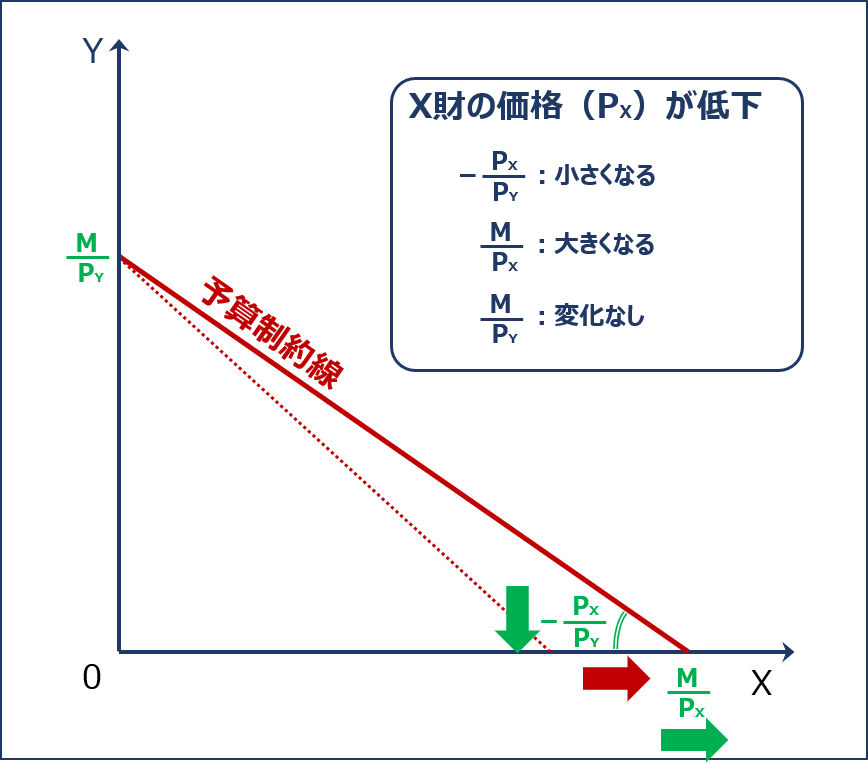
「X財の価格(PX)」が下落する場合の「予算制約線」のシフトについて確認します。
「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)( M ÷ PY )」は変わりませんが「Y財の消費量がゼロである場合のX財の消費量( M ÷ PX )」が大きくなり「予算制約線の傾きの絶対値( PX ÷ PY )」が小さくなるため、「予算制約線」は以下の通り右方にシフトします。
X財の価格が上昇する場合
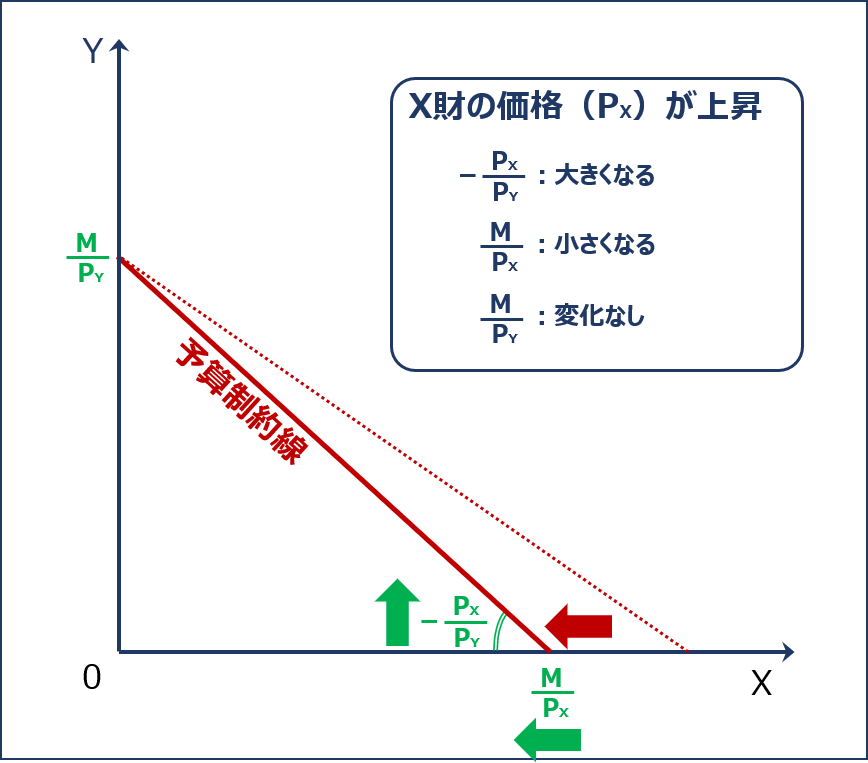
「X財の価格(PX)」が上昇する場合の「予算制約線」のシフトについて確認します。
「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)( M ÷ PY )」は変わりませんが「Y財の消費量がゼロである場合のX財の消費量( M ÷ PX )」が小さくなり「予算制約線の傾きの絶対値( PX ÷ PY )」が大きくなるため「予算制約線」は以下の通り左方にシフトします。
Y財の価格が変動する場合
Y財の価格が下落する場合
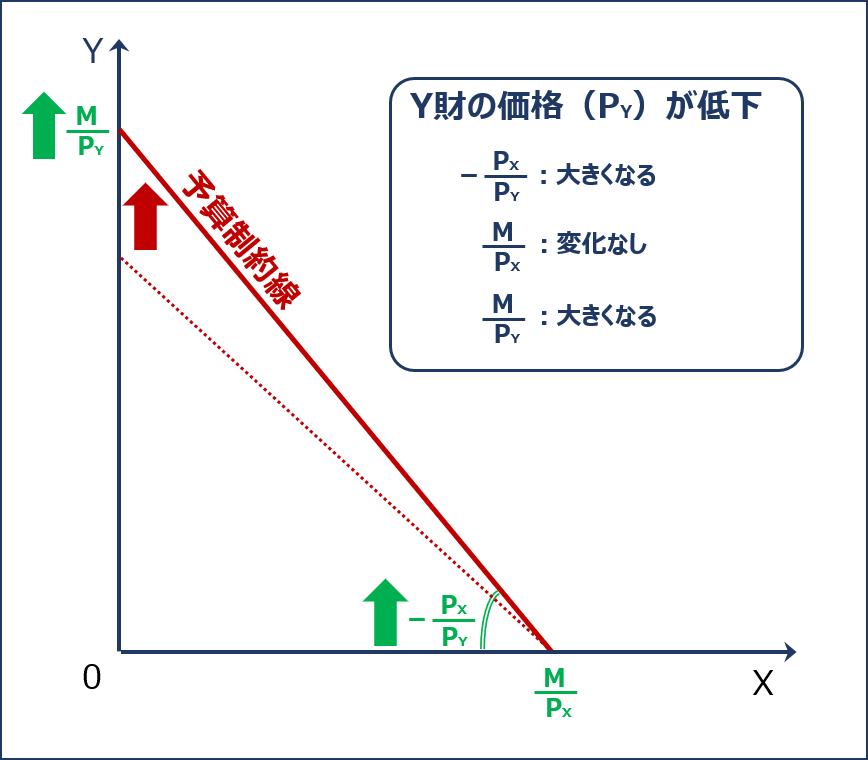
「Y財の価格(PY)」が下落する場合の「予算制約線」のシフトについて確認します。
「Y財の消費量がゼロである場合のX財の消費量( M ÷ PX )」は変わりませんが「予算制約線の傾きの絶対値( PX ÷ PY )」と「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)( M ÷ PY )」が大きくなるため、「予算制約線」は以下の通り上方にシフトします。
Y財の価格が上昇する場合
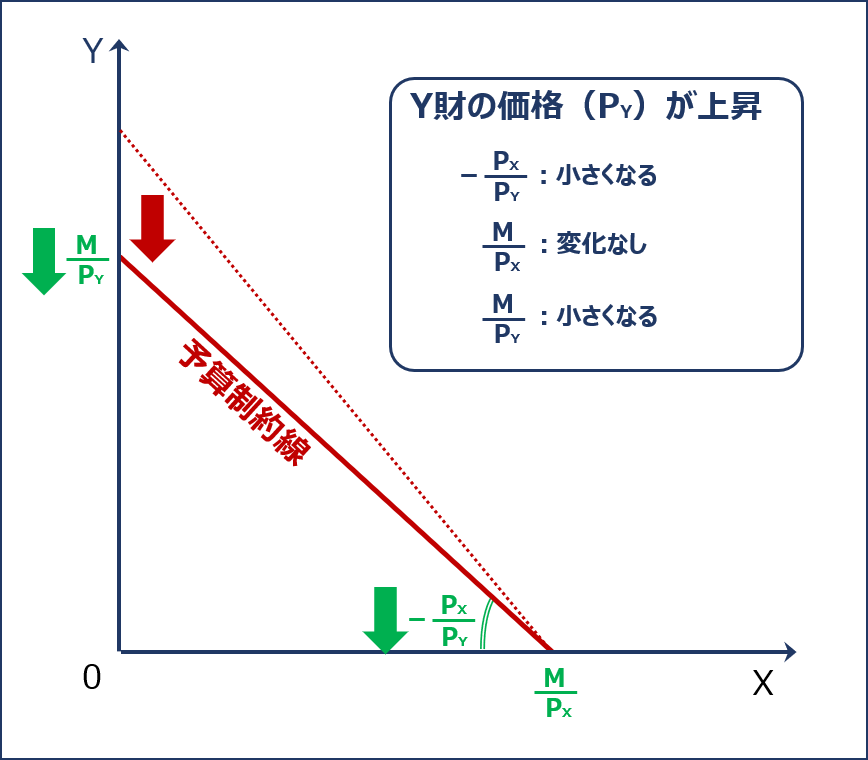
「Y財の価格(PY)」が上昇する場合の「予算制約線」のシフトについて確認します。
「Y財の消費量がゼロである場合のX財の消費量( M ÷ PX )」は変わりませんが「予算制約線の傾きの絶対値( PX ÷ PY )」と「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)( M ÷ PY )」が小さくなるため、「予算制約線」は以下の通り下方にシフトします。
予算が変動する場合
予算が増加する場合
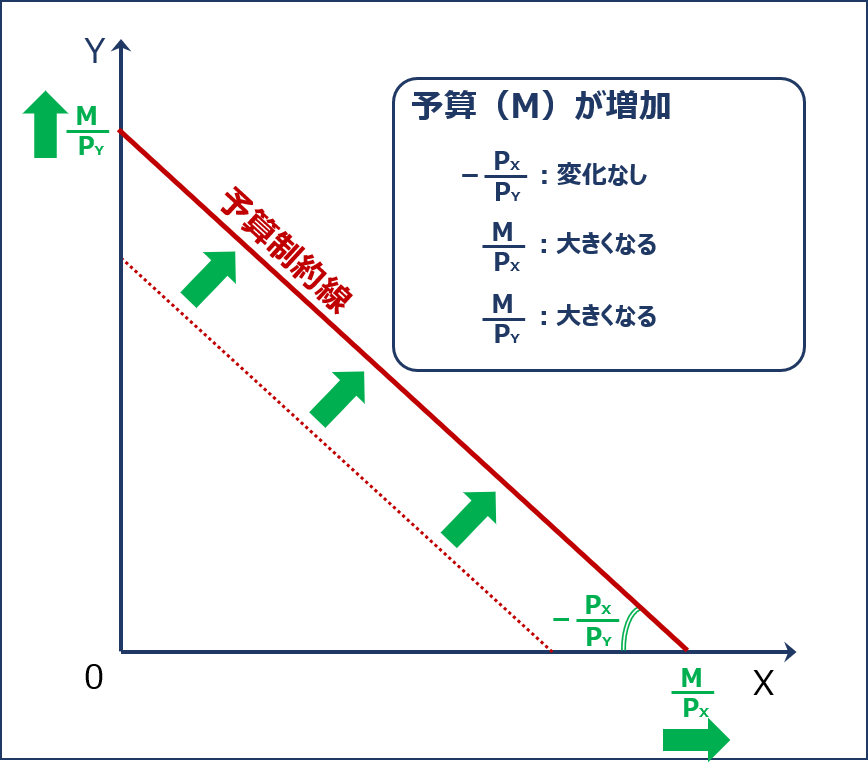
「予算(M)」が増加する場合の「予算制約線」のシフトについて確認します。
「予算制約線の傾きの絶対値( PX ÷ PY )」は変わりませんが「Y財の消費量がゼロである場合のX財の消費量( M ÷ PX )」と「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)( M ÷ PY )」が大きくなるため、「予算制約線」は以下の通り平行に右上方にシフトします。
予算が減少する場合
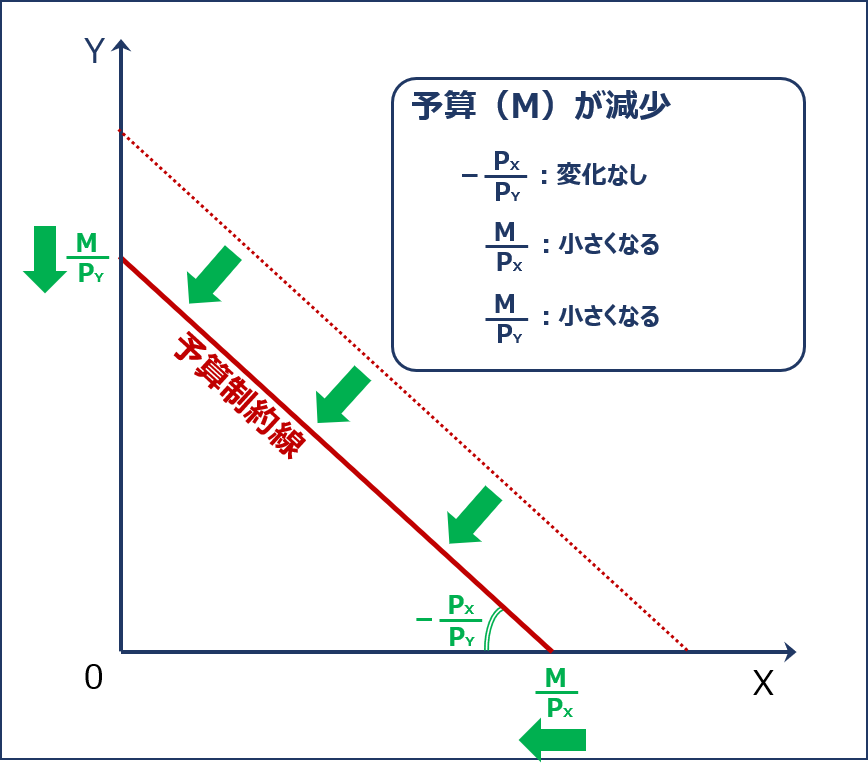
「予算(M)」が減少する場合の「予算制約線」のシフトについて確認します。
「予算制約線の傾きの絶対値( PX ÷ PY )」は変わりませんが「Y財の消費量がゼロである場合のX財の消費量( M ÷ PX )」と「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)( M ÷ PY )」が小さくなるため、「予算制約線」は以下の通り平行に左下方にシフトします。
最適消費点
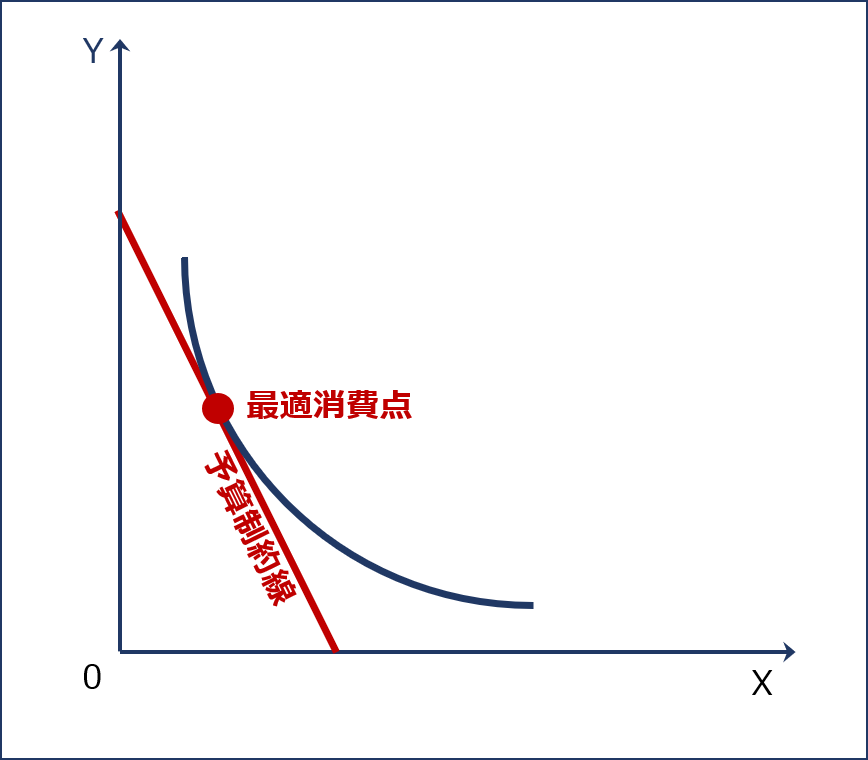
「最適消費点」とは、社会に2つの財しか存在しないという仮定の「2財モデル」において、「X財の消費量X」と「Y財の消費量Y」の2軸のグラフで表される「限られた予算の中で、ある消費者の効用を最大化する2財の消費の組み合わせを示す点」のことをいいます。
ある消費者が等しい効用を得られる2財の消費の組み合わせを表す「無差別曲線」と、予算を全て使い切った2財の消費の組み合わせを表す「予算制約線」の接点が「最適消費点」となります。
予約制約線の変化による最適消費点のシフト
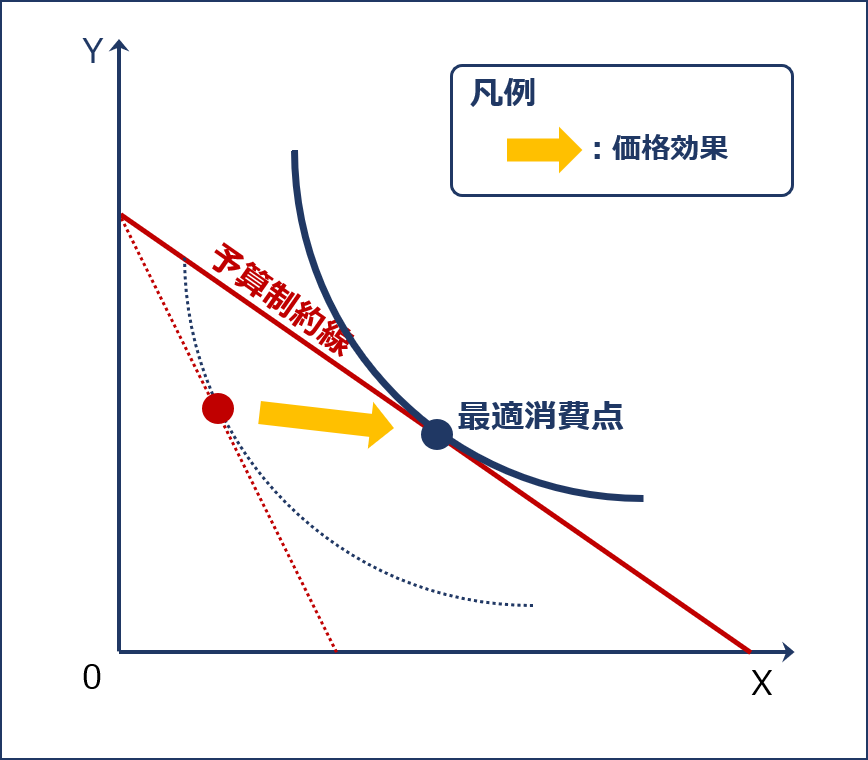
予約制約線の変化によって「最適消費点」がどのようにシフトするのかについて確認するため「X財の価格が下落した場合」を例として以下に説明します。
- X財の価格が下落すると「X財の消費量がゼロである場合のY財の消費量(Y軸の切片)」は変わらずに「Y財の消費量がゼロである場合のX財の消費量」が大きくなるため「予算制約線」が右方に拡大します。
- 拡大した「予算制約線」は、X財の価格が下落する前の「予約制約線」と接していた「無差別曲線」よりも効用が高い「無差別曲線」と接することとなるため、この新たな「無差別曲線」との接点が、X財の価格が下落した場合の「最適消費点」となります。(無差別曲線がシフトするわけではありません。もともと無差別曲線は無数に存在しています。)
価格効果(全部効果)
社会に2つの財しか存在しないという仮定の「2財モデル」において、財の価格変動が「最適消費点」に与える効果のことを「価格効果(全部効果)」といいます。
「価格効果(全部効果)」は、効用水準が一定という条件の下で2財の相対価格比の変化が「最適消費点」に与える効果である「代替効果」と、2財の相対価格比が一定という条件の下で実質取得の変化が「最適消費点」に与える効果である「所得効果」を掛け合わせた効果として表されます。
| 代替効果 | 効用水準が一定という条件の下で、2財の相対価格比の変化が最適消費点に与える効果 |
| 所得効果 | 2財の相対価格比が一定という条件の下で、実質取得の変化が最適消費点に与える効果 |
代替効果
「代替効果」とは、効用水準が一定という条件の下で、2財の相対価格比の変化が「最適消費点」に与える効果のことをいいます。
言葉の定義が難しいですが、X財の価格が下落すると、X財の方がY財より相対的に価格が安くなるため、Y財よりX財を購入するようになるという感覚だと理解すれば大丈夫だと思います。
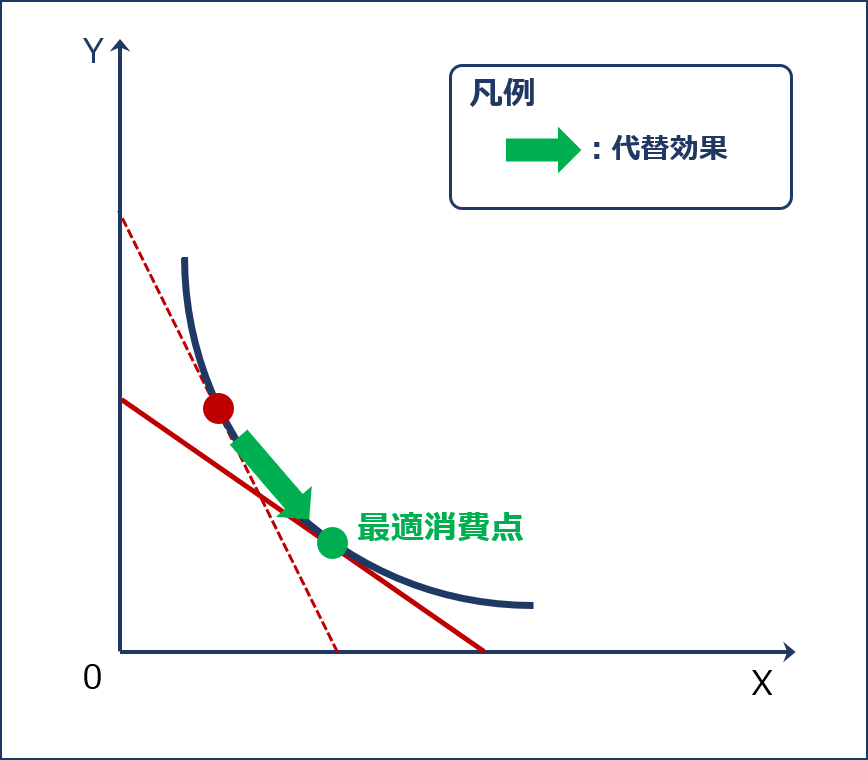
「代替効果」は、同一の「無差別曲線」に接する(効用水準が一定)ように「予算制約線」の傾きを変えながらシフトさせた(2財の相対価格比の変化)場合の「最適消費点」のシフトとして表されます。
「代替効果」のイメージ
所得効果
「所得効果」とは、2財の相対価格比が一定という条件の下で、実質取得の変化が最適消費点に与える効果のことをいいます。
言葉の定義が難しいですが、X財の価格の下落により「実質所得」が増加する(財を消費できる量が増加する)ため、2財を消費する量を増やすという感覚だと理解すれば大丈夫だと思います。
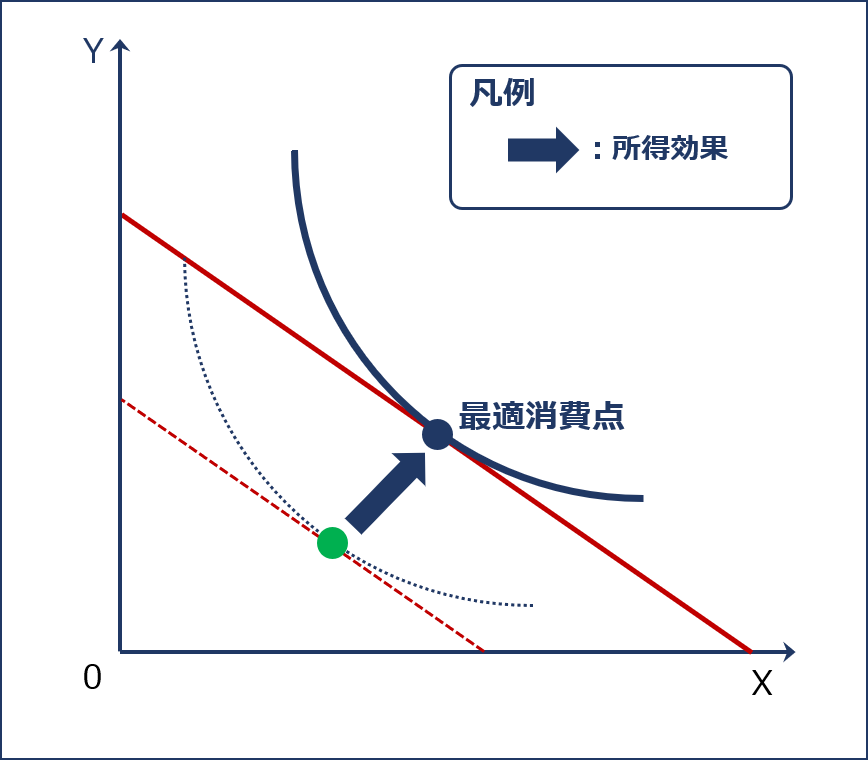
「所得効果」は、財の価格が変動した後の「予算制約線」を、傾きを変えず(2財の相対価格比が一定)に平行シフトさせた(実質取得の変化)場合の「最適消費点」のシフトとして表されます。
「所得効果」のイメージ
スルツキー分解
「スルツキー分解」とは、「価格効果(全部効果)」を「代替効果」と「所得効果」に分解することをいいます。
X財の価格が下落すると「予算制約線」がシフトして「最適消費点」もシフトします。
この「最適消費点のシフト(赤→青)」は、財の価格変動が「最適消費点」に与える効果である「価格効果(全部効果)」を表しています。

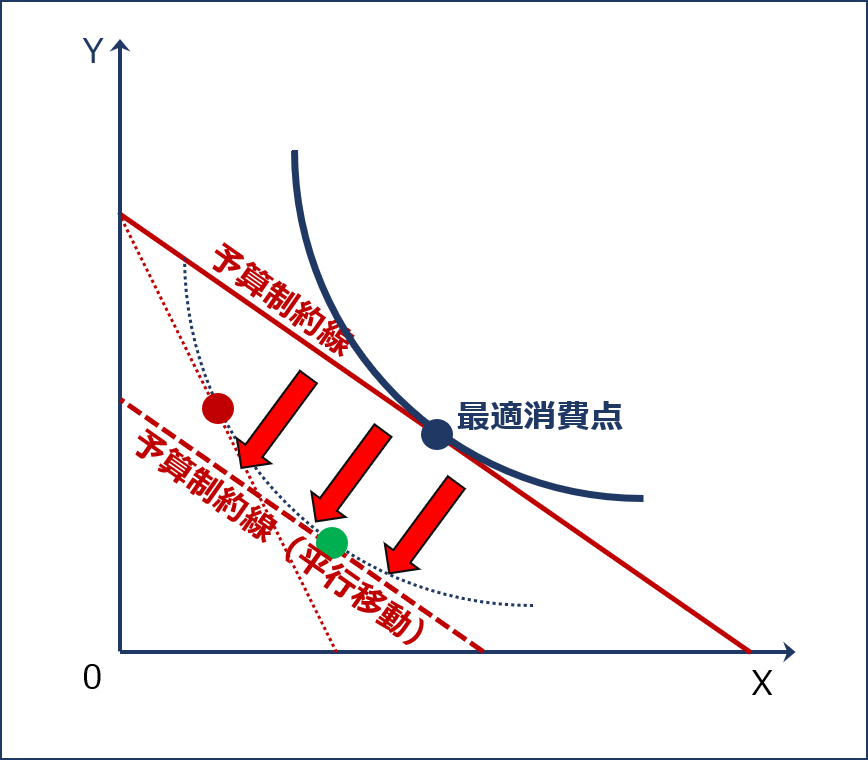
財の価格が変動した後の「予算制約線」を、傾きを変えず(2財の相対価格比が一定)に、X財の価格が下落する前の「予算制約線」が接していた「無差別曲線」と接する点(緑)まで平行シフト(実質取得の変化)します。
財の価格変動が「最適消費点」に与える効果である「価格効果(全部効果)」を、同一の「無差別曲線」に接する(効用水準が一定)ように「予算制約線」の傾きを変えながらシフトさせた(2財の相対価格比の変化)場合の「最適消費点」のシフトとして表される「代替効果(赤→緑)」と、財の価格が変動した後の「予算制約線」を、傾きを変えず(2財の相対価格比が一定)に平行シフトさせた(実質取得の変化)場合の「最適消費点」のシフトとして表される「所得効果(緑→青)」に分解することができました。
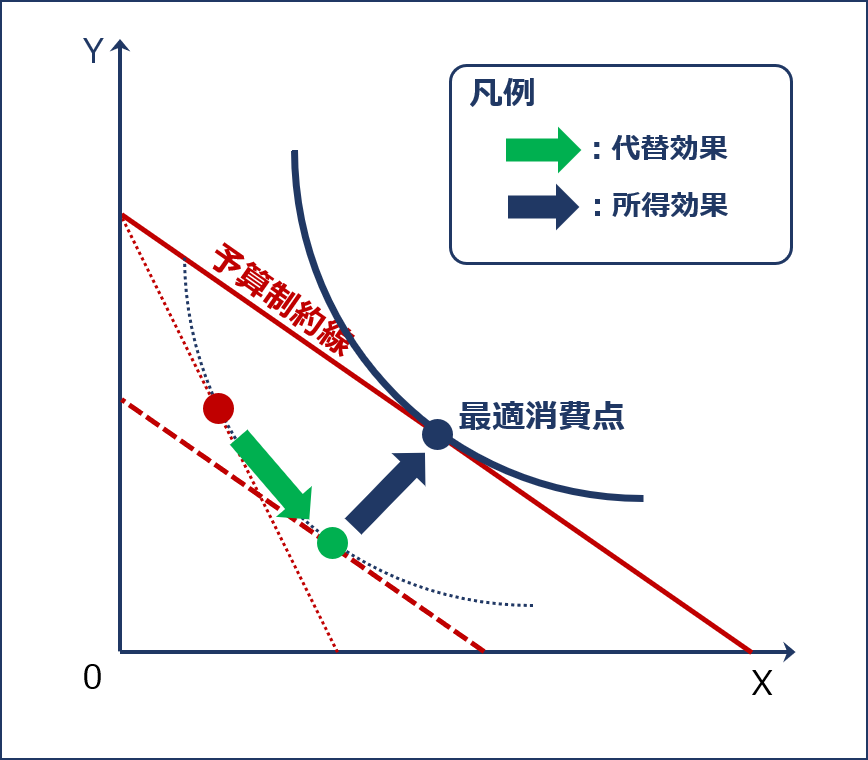
実際の問題では「スルツキー分解」が終わった後の図が示され、どれが「代替効果」と「所得効果」を表しているかという形で出題されます。
ギッフェン財
「ギッフェン財」とは「財の価格が下落(上昇)すると消費量が減少(増加)する財」のことをいいます。
「ギッフェン財」の事例としては、19世紀のアイルランドで発生したジャガイモ飢饉が有名です。
19世紀のアイルランドにおいて、貧しい人々の主食であるジャガイモ飢饉が発生して価格が高騰しましたが、人々は肉などの贅沢品の消費量を減少させ、主食であるジャガイモの消費量を増やしたというものです。
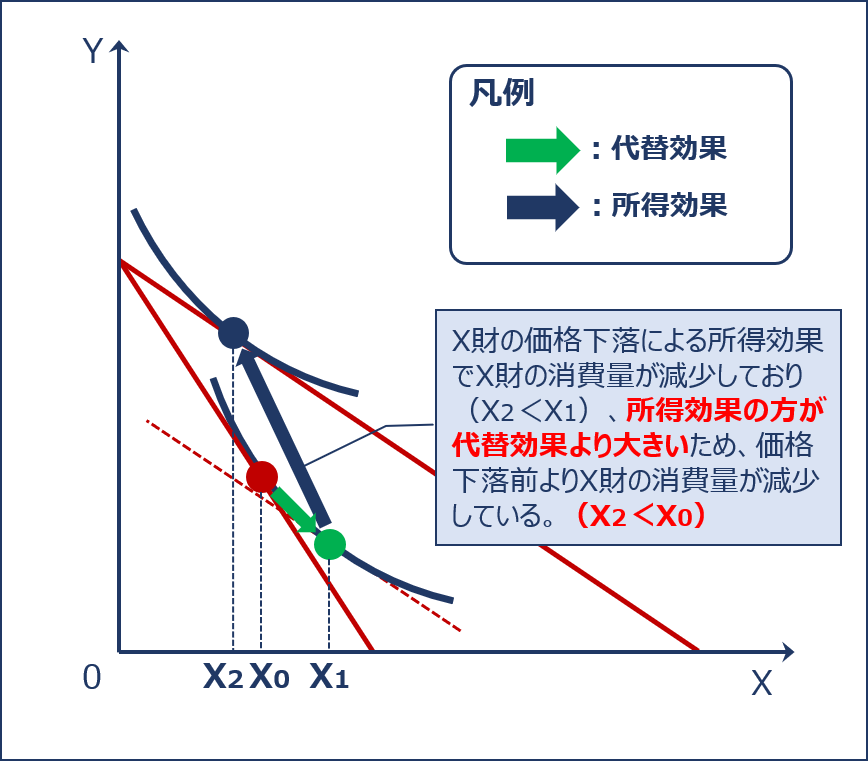
「ギッフェン財」であるX財の価格が下落した場合の「最適消費点」の変化を以下に示します。
ギッフェン財(価格効果)
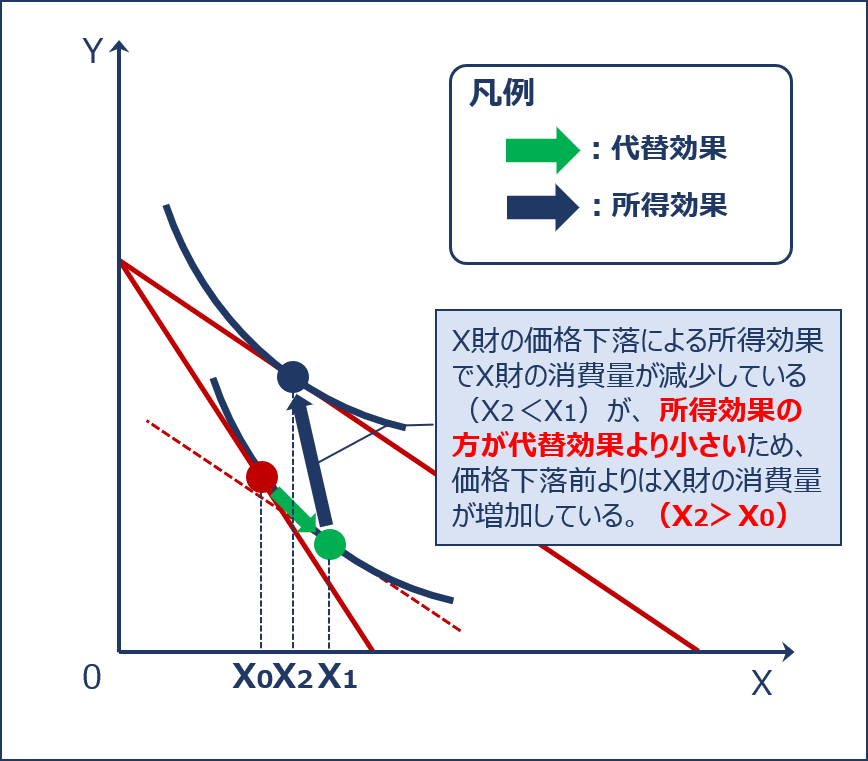
以下の図から分かるように「ギッフェン財」は「所得効果」の絶対値の方が「代替効果」の絶対値よりも大きい財のことをいいます。
ギッフェン財(代替効果と所得効果)

コメント