経済学･経済政策～等費用線･等産出量曲線（等量曲線）･費用最小化点のまとめ～

2021.05.28

今回は、「経済学･経済政策」の「等費用線」「等産出量曲線（等量曲線）」「費用最小化点」に関する記事のまとめです。

等費用線･等産出量曲線（等量曲線）･費用最小化点－リンク－
等費用線
1. 等費用線の求め方
2. 条件の変化に伴う等費用線のシフト
等産出量曲線（等量曲線）
1. 技術的限界代替率（MRTS）
費用最小化点
1. 等費用線の変化に伴う費用最小化点のシフト

等費用線･等産出量曲線（等量曲線）･費用最小化点－リンク－

本ブログにて「等費用線」「等産出量曲線（等量曲線）」「費用最小化点」について説明しているページを以下に示しますのでアクセスしてみてください。

等費用線

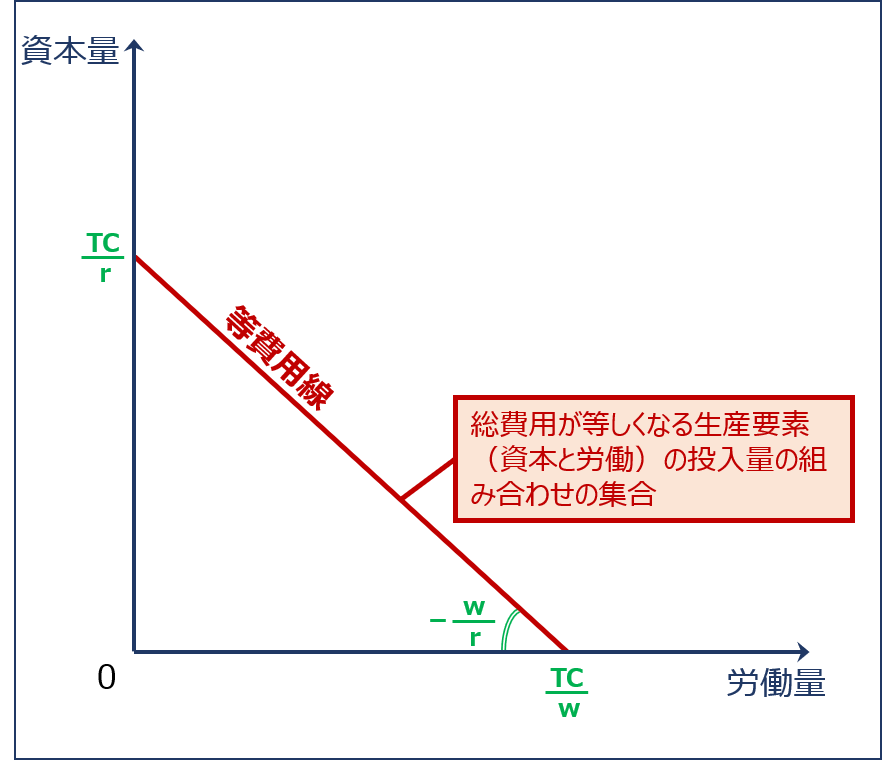
「等費用線」とは、生産活動において発生する費用である「資本」と「労働」という2つの生産要素を考えた場合、縦軸に「資本投入量」を、横軸に「労働投入量」を取ったグラフで表される「総費用が等しくなる生産要素（資本と労働）の投入量の組み合わせを結んだ曲線」のことをいいます。

「等費用線」は、企業の「予算制約線」とも言われており、消費者が予算を全て使い切る2財の消費の組み合わせを示す「予算制約線」と考え方は同じです。

等費用線

等費用線の求め方

「等費用線」の求め方について説明します。

生産活動において発生する「総費用（TC）」は、労働量の要素である「賃金率（w）」「労働投入量（L）」と、資本量の要素である「資本のレンタル価格（r）」「資本投入量（K）」を用いて、以下の式により求めることができます。

「等費用線」のグラフでは、縦軸に「資本投入量」を取るため、上記の式を「K＝」という形に変形した以下の式が「等費用線」を表しています。

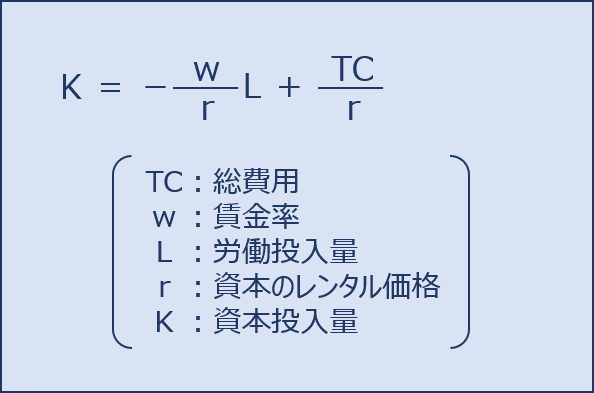
したがって「等費用線」は以下のように表すことができます。

等費用線

項目	説明	計算式
等費用線の傾き	生産要素（資本と労働）の価格比	w ÷ r
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC ÷ w
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC ÷ r

条件の変化に伴う等費用線のシフト

「賃金率（w）」「資本のレンタル価格（r）」「総費用（TC）」などの条件が変化すると「等費用線」はシフトします。

それぞれの条件が変化した場合に「等費用線」がどのようにシフトするのかを以下に説明していきます。

賃金率が変動する場合

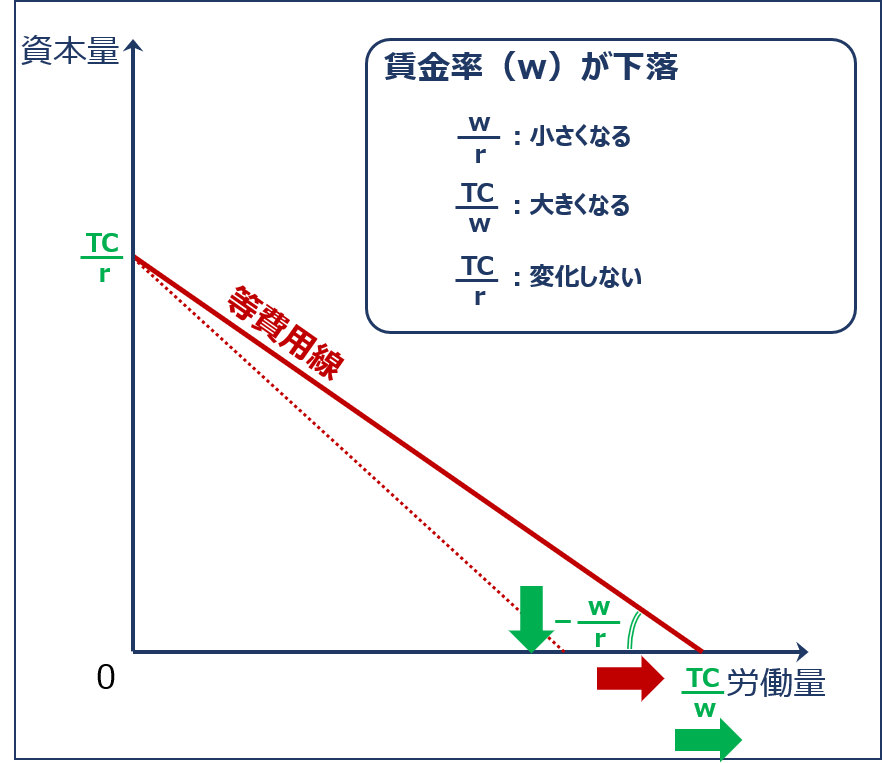
賃金率が下落する場合

「賃金率（w）」が下落すると、「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」は変わりませんが、「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」が大きくなり「等費用線の傾きの絶対値（ w ÷ r ）」が小さくなるため、「等費用線」は以下の通り右方に拡大します。

項目	説明	計算式	値の変化
等費用線の傾き	生産要素（資本と労働）の価格比	w↓ ÷ r	小さくなる↓
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC ÷ w↓	大きくなる↑
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC ÷ r	変化しない

賃金率が下落した場合

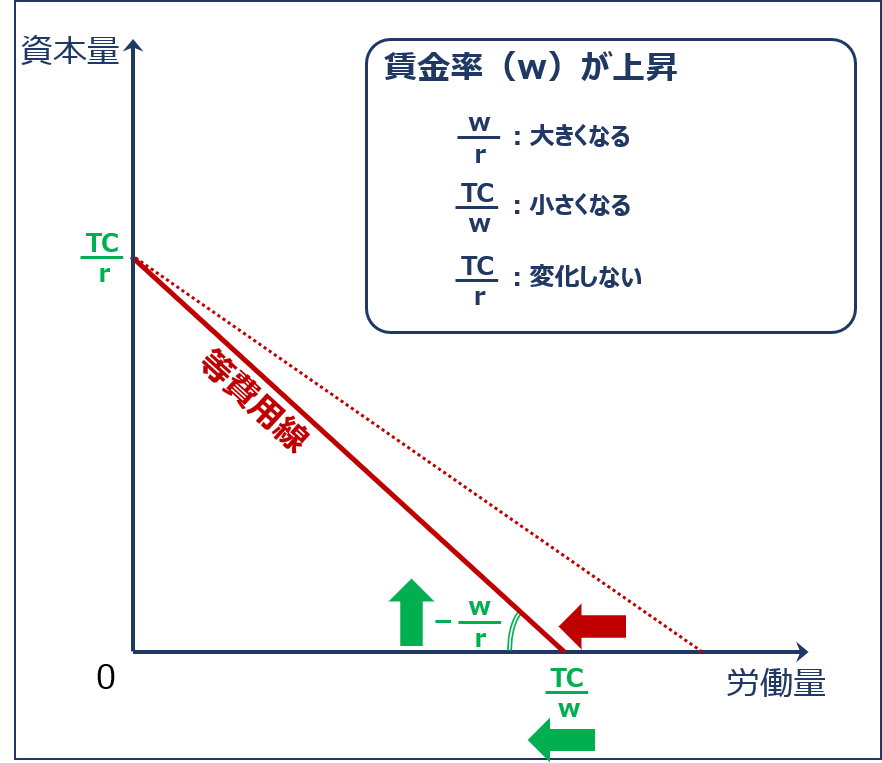
賃金率が上昇する場合

「賃金率（w）」が上昇すると、「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」は変わりませんが、「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」が小さくなり「等費用線の傾きの絶対値（ w ÷ r ）」が大きくなるため、「等費用線」は以下の通り左方に縮小します。

項目	説明	計算式	値の変化
等費用線の傾き	生産要素（資本と労働）の価格比	w↑ ÷ r	大きくなる↑
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC ÷ w↑	小さくなる↓
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC ÷ r	変化しない

賃金率が上昇した場合

資本のレンタル価格が変動する場合

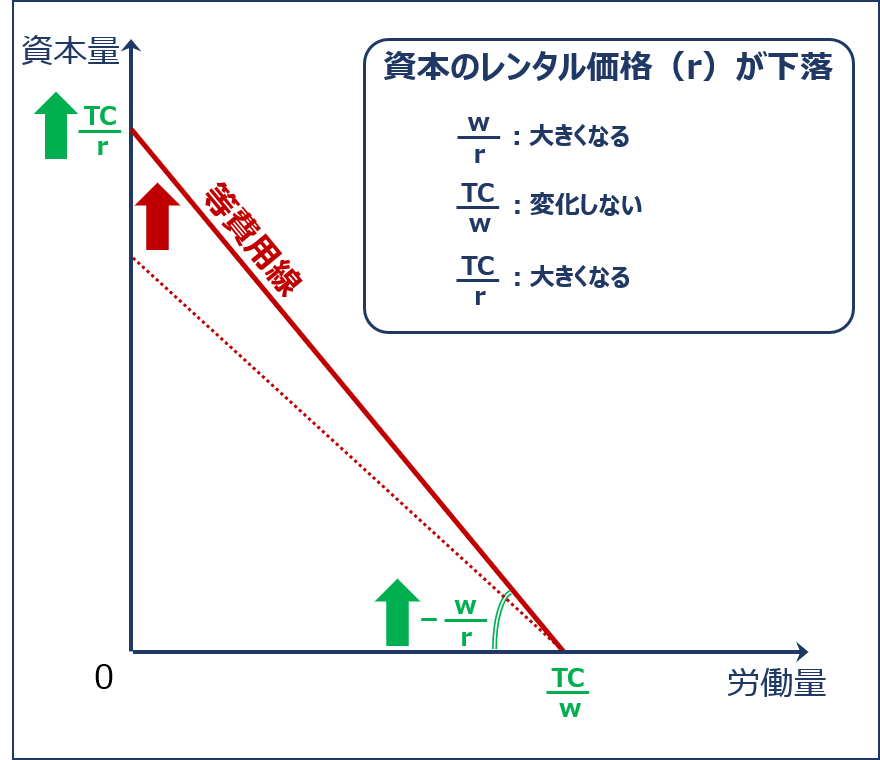
資本のレンタル価格が下落する場合

「資本のレンタル価格（r）」が下落すると、「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」は変わりませんが、「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」と「等費用線の傾きの絶対値（ w ÷ r ）」が大きくなるため、「等費用線」は以下の通り上方に拡大します。

項目	説明	計算式	値の変化
等費用線の傾き	生産要素（資本と労働）の価格比	w ÷ r↓	大きくなる↑
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC ÷ w	変化しない
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC ÷ r↓	大きくなる↑

資本のレンタル価格が下落した場合

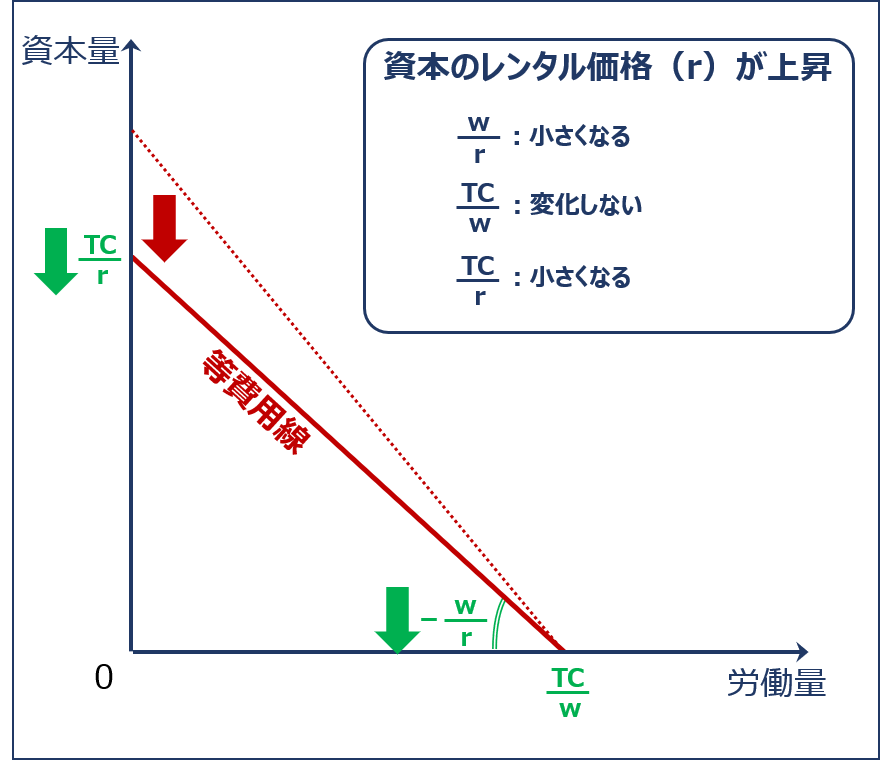
資本のレンタル価格が上昇する場合

「資本のレンタル価格（r）」が上昇すると、「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」は変わりませんが、「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」と「等費用線の傾きの絶対値（ w ÷ r ）」が小さくなるため、「等費用線」は以下の通り下方に縮小します。

項目	説明	計算式	値の変化
等費用線の傾き	生産要素（資本と労働）の価格比	w ÷ r↑	小さくなる↓
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC ÷ w	変化しない
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC ÷ r↑	小さくなる↓

資本のレンタル価格が上昇した場合

総費用が変動する場合

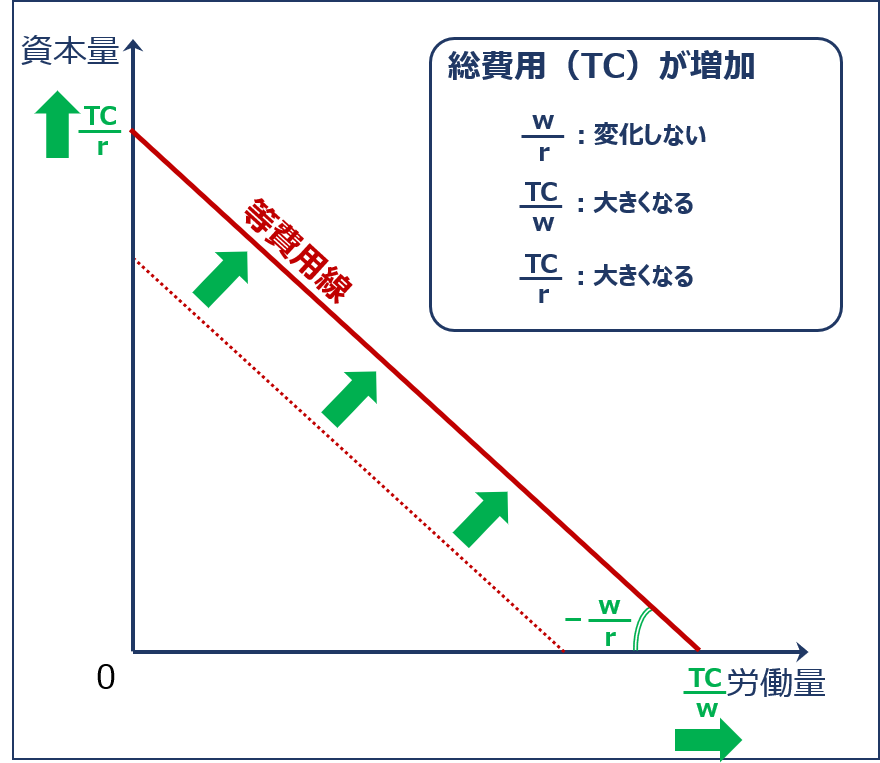
総費用が増加する場合

「総費用（TC）」が増加すると、「等費用線の傾きの絶対値（ w ÷ r ）」は変わりませんが、「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」と「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」が大きくなるため、「等費用線」は以下の通り右上方に平行シフトします。

項目	説明	計算式	値の変化
等費用線の傾き	生産要素（資本と労働）の価格比	w ÷ r	変化しない
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC↑ ÷ w	大きくなる↑
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC↑ ÷ r	大きくなる↑

総費用が増加した場合

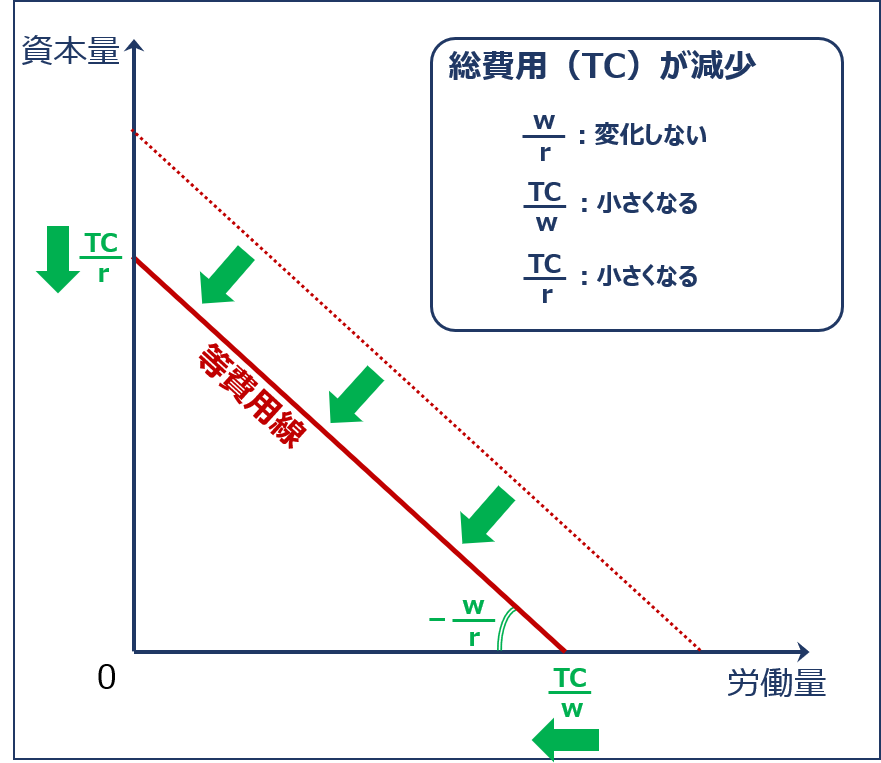
総費用が減少する場合

「総費用（TC）」が減少すると、「等費用線の傾きの絶対値（ w ÷ r ）」は変わりませんが、「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」と「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」が小さくなるため、「等費用線」は以下の通り左下方に平行シフトします。

項目	説明	計算式	値の変化
等費用線の傾き	生産要素（資本と労働）の価格比	w ÷ r	変化しない
横軸の切片	資本の投入量がゼロである場合の労働の投入量	TC↓ ÷ w	小さくなる↓
縦軸の切片	労働の投入量がゼロである場合の資本の投入量	TC↓ ÷ r	小さくなる↓

総費用が減少した場合

等産出量曲線（等量曲線）

「等産出量曲線（等量曲線）」とは、生産活動において発生する費用である「資本」と「労働」という2つの生産要素を考えた場合、縦軸に「資本投入量」を、横軸に「労働投入量」を取ったグラフで表される「産出量が等しくなる生産要素（資本と労働）の投入量の組み合わせを結んだ曲線」のことをいいます。

「等産出量曲線（等量曲線）」では「同一の等産出量曲線（等量曲線）上においてはどの点を取っても産出量は等しい」という特徴を理解しておくことが重要です。

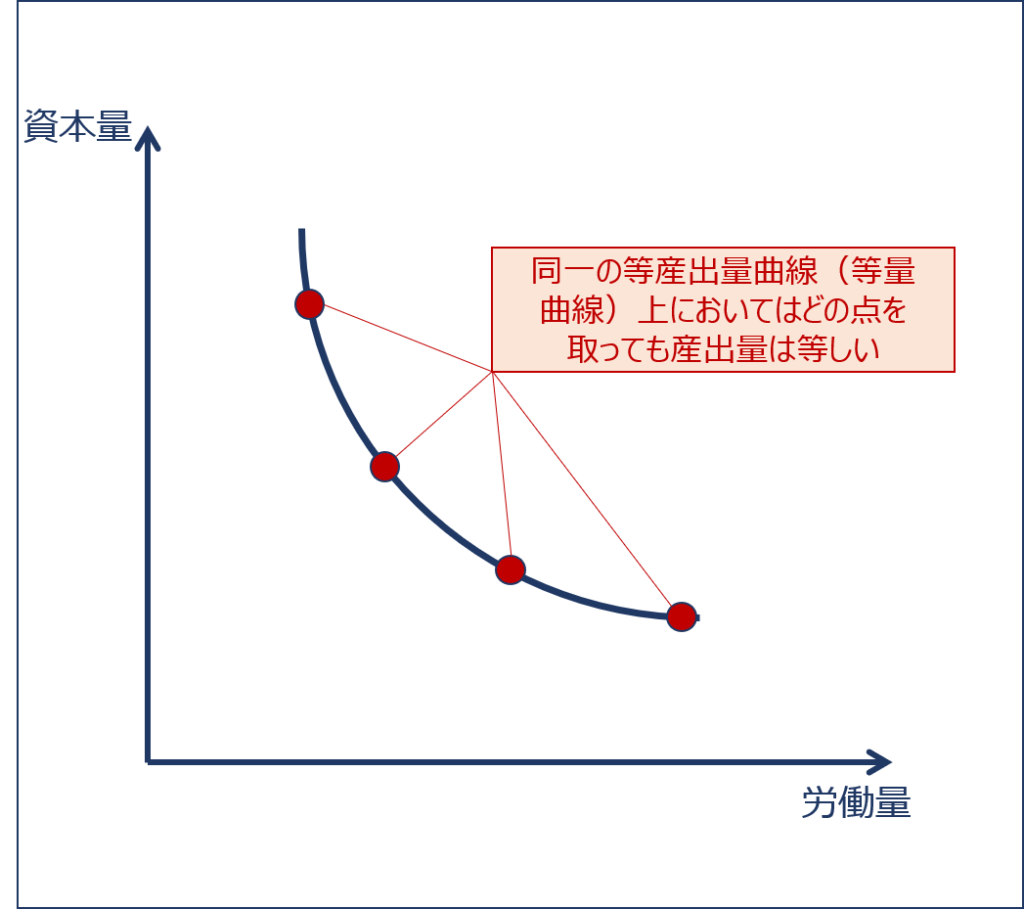
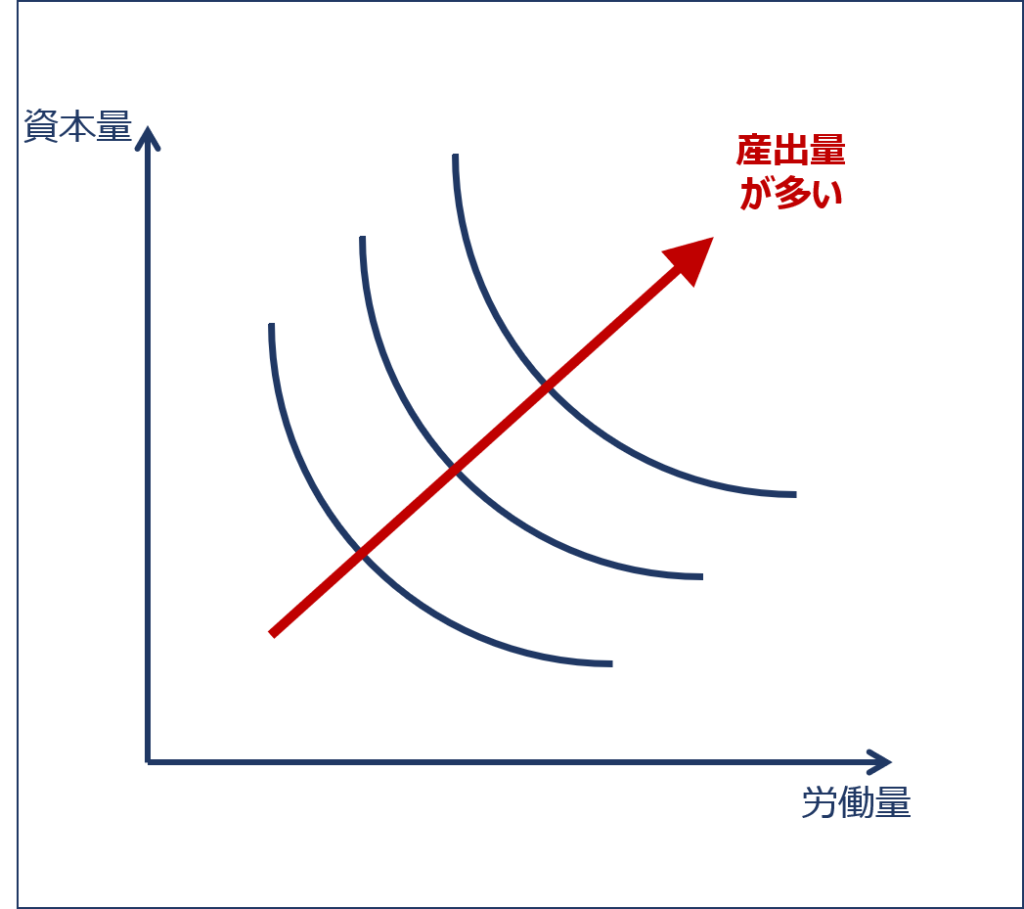
「等産出量曲線（等量曲線）」は、消費者が等しい効用を得られる2財の消費の組み合わせを示す「無差別曲線」と考え方は同じです。

等産出量曲線（等量曲線）

また、「等産出量曲線（等量曲線）」は以下の図のように「3本」しかないわけではなく無数に存在しており、右上にある「等産出量曲線（等量曲線）」ほど産出量が多いという特徴も理解しておくことが重要です。

技術的限界代替率（MRTS）

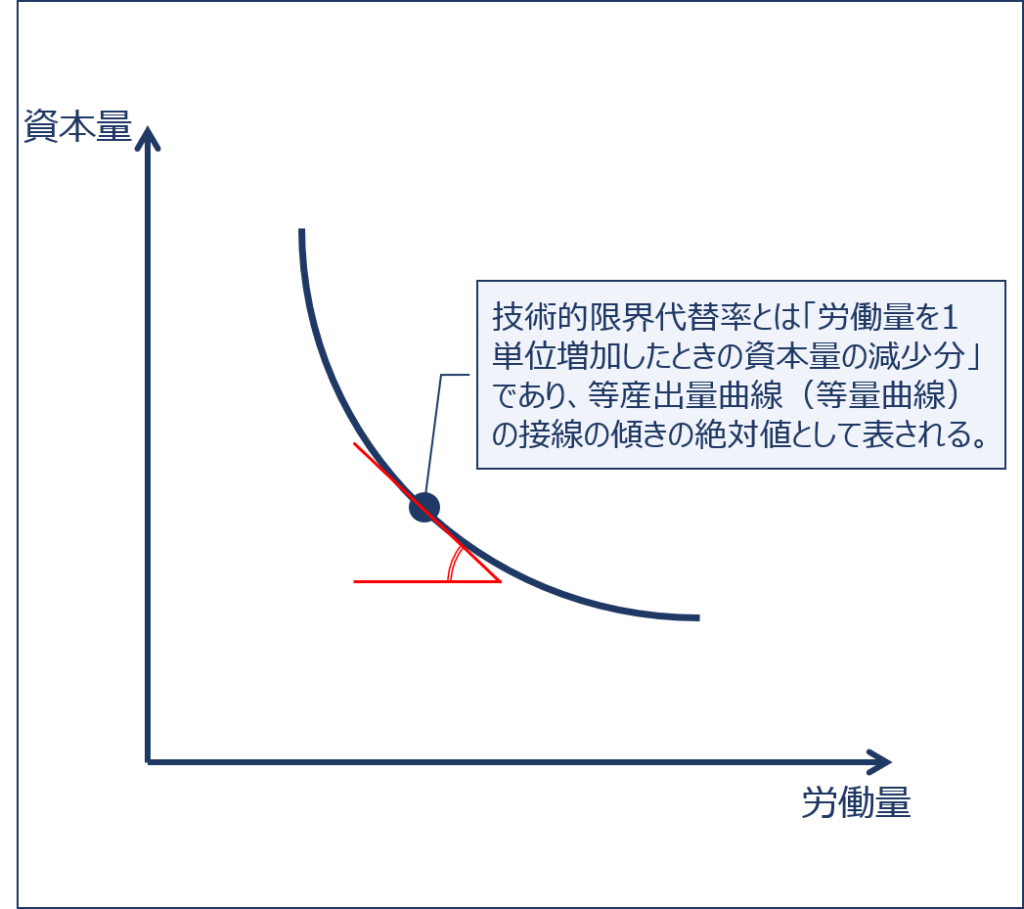
「技術的限界代替率」とは、生産活動において発生する費用である「資本」と「労働」という2つの生産要素を考えた場合、縦軸に「資本投入量」を、横軸に「労働投入量」を取ったグラフで表される「産出量が一定であるという条件において、労働投入量を1単位増加したときの資本投入量の減少分」のことをいい、「等産出量曲線（等量曲線）」の接線の傾きの絶対値として表されます。

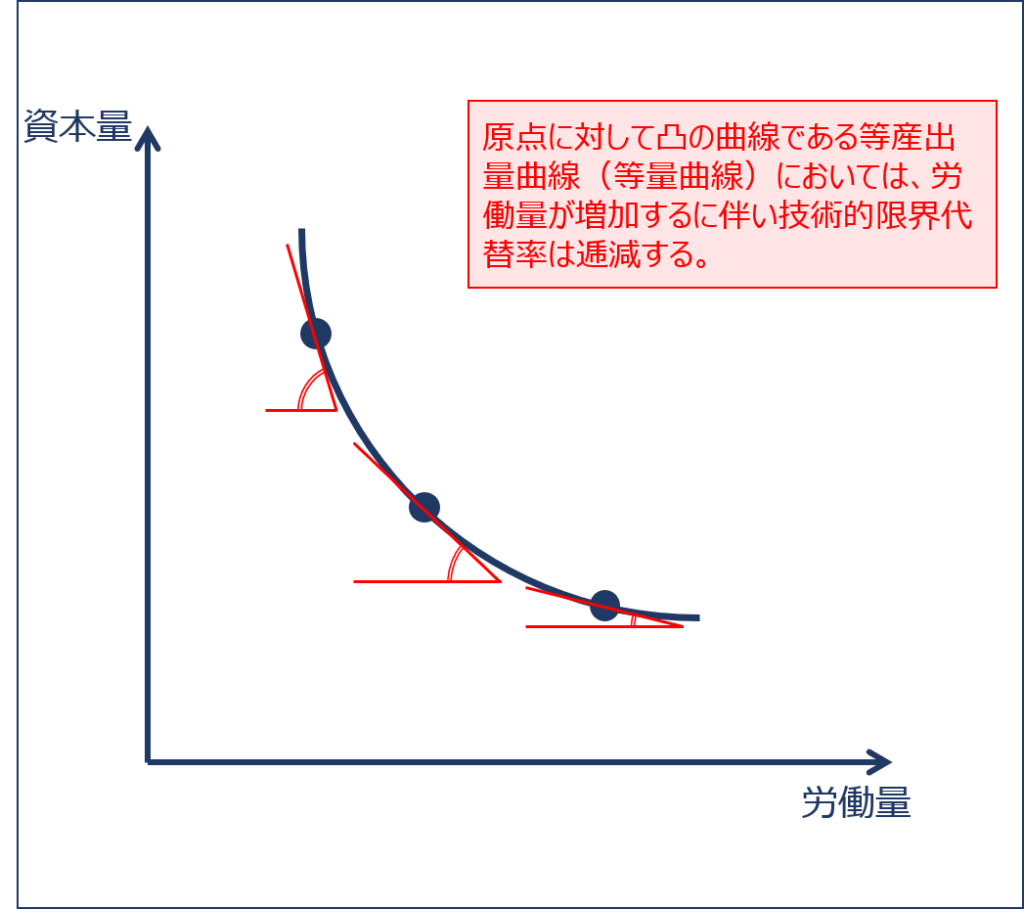
「等産出量曲線（等量曲線）」は、原点に対して凸の形状をした曲線であり、労働投入量の増加に伴い「技術的限界代替率」が徐々に減少していきます（逓減する）。

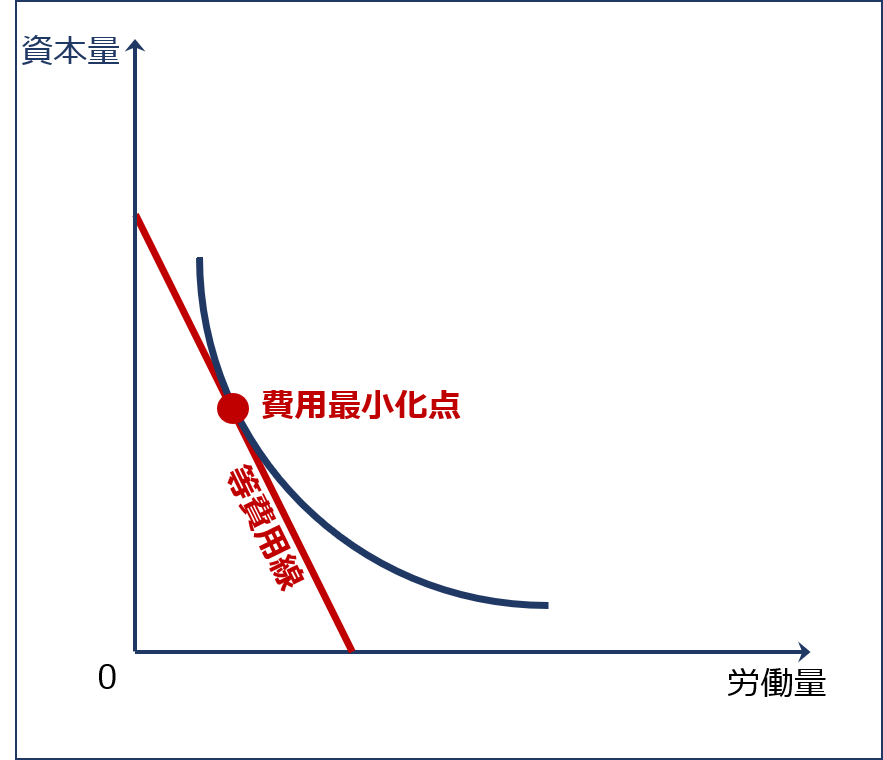
「技術的限界代替率」は、消費者が得られる効用水準が一定という条件において、X財の消費を1単位増加したときのY財の消費の減少分を示す「限界代替率」と考え方は同じです。

費用最小化点

「費用最小化点」とは、生産活動において発生する費用である「資本」と「労働」という2つの生産要素を考えた場合、縦軸に「資本投入量」を、横軸に「労働投入量」を取ったグラフで表される「ある産出量を生産するための総費用を最小化する生産要素（資本と労働）の投入量の組み合わせを示す点」のことをいい、「等費用線」と「等産出量曲線（等量曲線）」の接点として表されます。

「費用最小化点」は、限られた予算の中で、ある消費者の効用を最大化する2財の消費の組み合わせを示す「最適消費点」と考え方は同じです。

費用最小化点

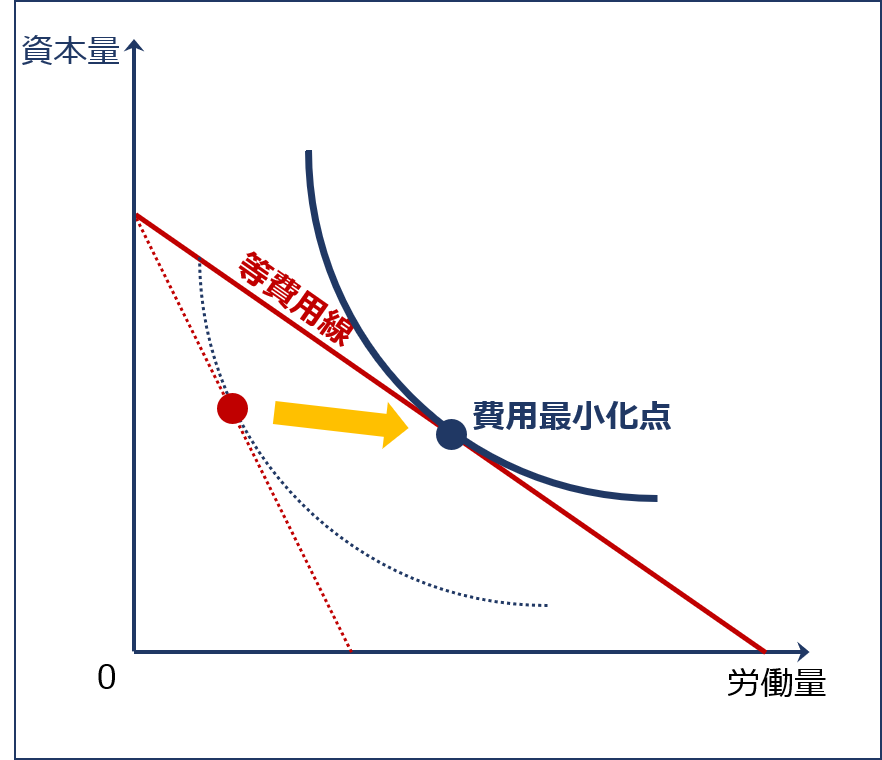
等費用線の変化に伴う費用最小化点のシフト

「等費用線」の変化によって「費用最小化点」がどのようにシフトするのかについて確認するため「賃金率が下落した場合」を例として以下に説明します。

「賃金率（w）」が下落すると、「労働の投入量がゼロである場合の資本の投入量（縦軸の切片）（ TC ÷ r ）」は変わりませんが「資本の投入量がゼロである場合の労働の投入量（横軸の切片）（ TC ÷ w ）」が大きくなるため「等費用線」も右方に拡大します。
右方に拡大した「等費用線」は「賃金率（w）」が下落する前の「等費用線」が接していた「等産出量曲線（等量曲線）」よりも産出量が多い、新たな「等産出量曲線（等量曲線）」と接します。（等産出量曲線（等量曲線）がシフトするわけではありません。もともと等産出量曲線（等量曲線）は無数に存在しています。）
この新たな「等産出量曲線（等量曲線）」と右方に拡大した「等費用線」との接点が「総費用（TC）」が増加した場合の「費用最小化点」となります。