今回は、「経済学・経済政策 ~H28-11-1 IS-LM曲線(7)IS曲線とLM曲線の傾き~」について説明します。
目次
経済学・経済政策 ~平成28年度一次試験問題一覧~
平成28年度の試験問題に関する解説は、以下のページを参照してください。
IS-LM曲線 -リンク-
本ブログにて「IS-LM曲線」について説明しているページを以下に示しますのでアクセスしてみてください。
- IS-LM曲線のまとめ
- R5-8-1 IS-LM曲線(14)IS曲線
- R3-6-1 IS-LM曲線(12)垂直のLM曲線
- R3-6-2 IS-LM曲線(13)財政政策と金融政策の効果
- R2-6-1 IS-LM曲線(1)垂直のIS曲線
- R2-6-2 IS-LM曲線(2)財政政策と金融政策の効果
- R1-8-1 IS-LM曲線(3)水平なLM曲線
- R1-8-2 IS-LM曲線(4)財政政策と金融政策の効果
- H29-9-1 IS-LM曲線(5)超過需要と超過供給
- H29-9-2 IS-LM曲線(6)公債の資産効果
- H28-11-2 IS-LM曲線(8)財政政策の効果
- H27-6 IS-LM曲線(9)財政政策の効果
- H26-5 IS-LM曲線(10)財政政策の効果
- H24-9 IS-LM曲線(11)IS曲線とLM曲線の形状とシフト
IS曲線とは
「IS曲線」とは、縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「財市場」が均衡する点の組み合わせを表す曲線のことをいいます。
「財市場」において「利子率(r)」が低下すると「投資(I)」が増加して「均衡GDP(YE)」が増加するため「IS曲線」は右下がりの曲線として表されます。
なお、「IS曲線」の「I」は「Investment(投資)」を、「S」は「Savings(貯蓄)」を表しています。
IS曲線

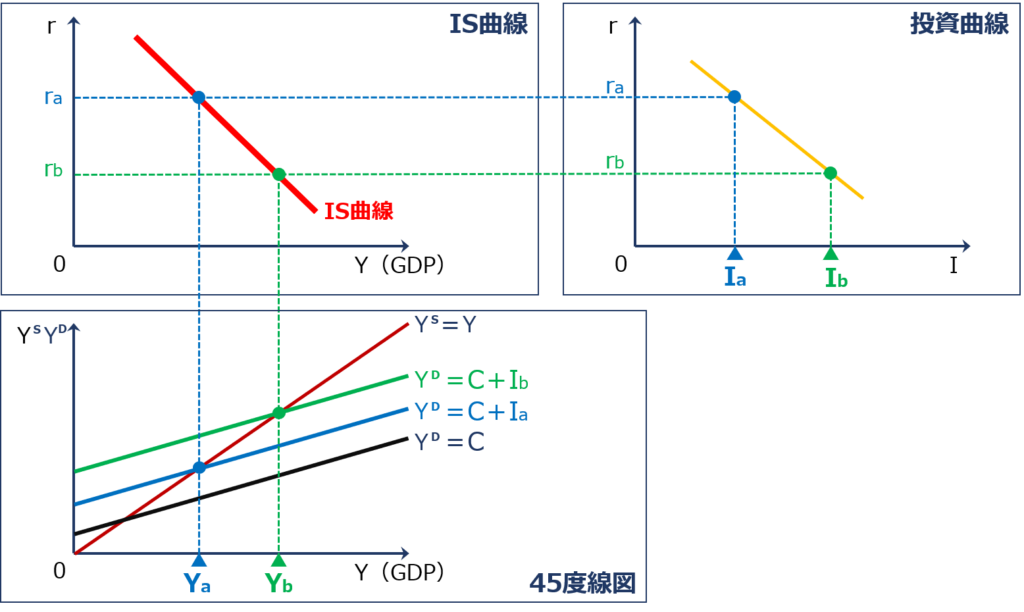
IS曲線の描写
「IS曲線」は、縦軸に「利子率(r)」を、横軸に「投資(I)」を取った「投資曲線」と、縦軸に「総供給(YS)、総需要(YD)」を、横軸に「GDP(Y)」を取った「45度線図」を用いて、「利子率(r)」が変化したときに「GDP(Y)」がどのように変化するのかを確認することで描写することができます。
結論として、「利子率(r)」が低下すると「均衡GDP(YE)」が増加するため「IS曲線」は右下がりの曲線として表されます。
「利子率(r)」が低下した場合に「均衡GDP(YE)」が変化していく流れを以下に示します。
- 「利子率(r)」が「ra」から「rb」に低下する
- 「利子率(r)」が低下したため「投資(I)」が「Ia」から「Ib」に増加する
- 「投資(I)」が増加したため「 Y=C+I 」で表される「総需要(YD)」が「Ya」から「Yb」に増加する
- 「総需要(YD)」が増加したため、企業が増産して「総供給(YS)」も「Ya」から「Yb」に増加して「財市場」が均衡する。
IS曲線の描写
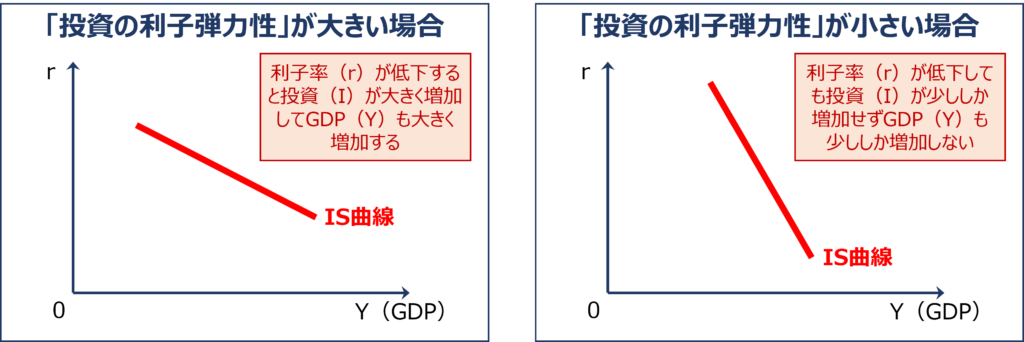
投資の利子弾力性の大きさによるIS曲線の傾きの変化
「IS曲線」の傾きは「投資の利子弾力性」の大きさにより変化します。
「投資の利子弾力性」とは「利子率(r)」が変動したときに「投資(I)」がどれだけ反応するかを表しています。
「投資の利子弾力性」が大きい場合は「利子率(r)」が少し低下するだけで「投資(I)」が大きく増加するため「総需要(YD)」が一気に増加して「均衡GDP(YE)」も大きく増加します。
逆に「投資の利子弾力性」が小さい場合は「利子率(r)」が大きく低下しても「投資(I)」は少ししか増加しないため「総需要(YD)」が少ししか増加せず「均衡GDP(YE)」も少ししか増加しません。
そのため、「投資の利子弾力性」が大きい場合は「IS曲線」の傾きは緩やかになり、「投資の利子弾力性」が小さい場合は「IS曲線」の傾きは急になります。
投資の利子弾力性が無限大の場合
極端な例として、「投資の利子弾力性」が無限大の場合は「利子率(r)」が少しでも低下すると「投資(I)」は一気に増加するため「総需要(YD)」が一気に増加して「均衡GDP(YE)」も一気に増加します。その結果、「IS曲線」は、水平の曲線として表されます。
投資の利子弾力性が無限大の場合

投資の利子弾力性がゼロの場合(投資が利子非弾力性な場合)
逆に、「投資の利子弾力性」がゼロの場合(投資が利子非弾力性な場合)は「利子率(r)」が低下しても「投資(I)」は一切増加しなくなるため「総需要(YD)」が一切増加せず「均衡GDP(YE)」も一切増加しません。その結果、「IS曲線」は、垂直の曲線として表されます。
投資の利子弾力性がゼロの場合

IS曲線の傾きとY軸の切片
具体的な関数を用いて「IS曲線」の「傾き」と「Y軸の切片」を考えていきます。
「IS曲線」は、縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフであるため、以下の関数で表すことができます。なお、「IS曲線」は右下がりの曲線であるため「傾き」はマイナスです。
- r = -●Y + ■(傾き:●、Y軸の切片:■)
例として「閉鎖経済/開放経済」と「税金を考慮しない場合/税金(定額税)を考慮した場合」を組み合わせた4パターンについて「IS曲線」を表す関数を求め、その「傾き」と「Y軸の切片」の関係を確認していきます。
なお、以下に示す内容を暗記するのではなく、試験問題において「総需要曲線」「消費(C)」「投資(I)」などの関数が与えられた場合は、試験問題で与えられた関数から「IS曲線」を表す関数を求め、「傾き」と「Y軸の切片」の関係を確認してください。
閉鎖経済(税金を考慮しない場合)
「閉鎖経済」において「総需要曲線(YD)」と「総供給曲線(YS)」を表す関数は以下の通りです。(C:消費、I:投資、G:政府支出、Y:GDP)
- YD = C + I + G
- YS = Y
「IS曲線」は「財市場」が均衡する点の組み合わせを表しているため「YD = YS」の関係が成立します。
- Y = C + I + G
「消費(C)」「投資(I)」「政府支出(G)」が以下の関数で与えられている場合
- C = a + bY(a:基礎消費、b:限界消費性向、Y:GDP)
- I = I0 - I1r(I0:独立投資、I1:投資の利子弾力性、r:利子率)
- G = G0(G0:政府支出)
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフである「IS曲線」を表す関数は以下の通りとなります。
- Y = a + bY + I0 - I1r + G0
- I1r = -( 1 - b )Y +( a + I0 + G0 )
- r = -( 1 - b )÷ I1 × Y +( a + I0 + G0 )÷ I1

「IS曲線」を表す関数から、財市場の変動要素による「傾き」と「Y軸の切片」の変化を整理すると以下の通りとなります。
IS曲線の傾き
- 「限界消費性向(b)」の値が大きくなると傾きが緩やかになる
- 「投資の利子弾力性(I1)」の値が大きくなると傾きが緩やかになる
IS曲線のY軸の切片
- 「基礎消費(a)」の値が大きくなるとY軸の切片が大きくなる
- 「独立投資(I0)」の値が大きくなるとY軸の切片が大きくなる
- 「政府支出(G0)」の値が大きくなるとY軸の切片が大きくなる
- 「投資の利子弾力性(I1)」の値が大きくなるとY軸の切片が小さくなる
閉鎖経済(税金(定額税)を考慮する場合)
「閉鎖経済」において「総需要曲線(YD)」と「総供給曲線(YS)」を表す関数は以下の通りです。(C:消費、I:投資、G:政府支出、Y:GDP)
- YD = C + I + G
- YS = Y
「IS曲線」は「財市場」が均衡する点の組み合わせを表しているため「YD = YS」の関係が成立します。
- Y = C + I + G
「消費(C)」「投資(I)」「政府支出(G)」が以下の関数で与えられている場合
- C = a + b( Y - T0 )(a:基礎消費、b:限界消費性向、Y:GDP、T0:定額税)
- I = I0 - I1r(I0:独立投資、I1:投資の利子弾力性、r:利子率)
- G = G0(G0:政府支出)
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフである「IS曲線」を表す関数は以下の通りとなります。
- Y = a + b( Y - T0 )+ I0 - I1r + G0
- I1r = -( 1 - b )Y +( a - bT0 + I0 + G0 )
- r = -( 1 - b )÷ I1 × Y +( a - bT0 + I0 + G0 )÷ I1

「IS曲線」を表す関数から、財市場の変動要素による「傾き」と「Y軸の切片」の変化を整理すると以下の通りとなります。
IS曲線の傾き
- 「限界消費性向(b)」の値が大きくなると傾きが緩やかになる
- 「投資の利子弾力性(I1)」の値が大きくなると傾きが緩やかになる
IS曲線のY軸の切片
- 「基礎消費(a)」の値が大きくなるとY軸の切片が大きくなる
- 「限界消費性向(b)」の値が大きくなるとY軸の切片が小さくなる
- 「定額税(T0)」の値が大きくなるとY軸の切片が小さくなる
- 「独立投資(I0)」の値が大きくなるとY軸の切片が大きくなる
- 「政府支出(G0)」の値が大きくなるとY軸の切片が大きくなる
- 「投資の利子弾力性(I1)」の値が大きくなるとY軸の切片が小さくなる
開放経済(税金を考慮しない場合)
「開放経済」において「総需要曲線(YD)」と「総供給曲線(YS)」を表す関数は以下の通りです。(C:消費、I:投資、G:政府支出、EX:輸出、IM:輸入、Y:GDP)
- YD = C + I + G + EX - IM
- YS = Y
「IS曲線」は「財市場」が均衡する点の組み合わせを表しているため「YD = YS」の関係が成立します。
- Y = C + I + G + EX - IM
「消費(C)」「投資(I)」「政府支出(G)」「輸出(EX)」「輸入(IM)」が以下の関数で与えられている場合
- C = a + bY(a:基礎消費、b:限界消費性向、Y:GDP)
- I = I0 - I1r(I0:独立投資、I1:投資の利子弾力性、r:利子率)
- G = G0(G0:政府支出)
- EX = EX0(EX0:輸出)
- IM = mY(m:限界輸入性向、Y:GDP)
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフである「IS曲線」を表す関数は以下の通りとなります。
- Y = a + bY + I0 - I1r + G0 + EX0 - mY
- I1r = -( 1 - b + m )Y +( a + I0 + G0 + EX0 )
- r = -( 1 - b + m )÷ I1 × Y +( a + I0 + G0 + EX0 )÷ I1

「IS曲線」を表す関数から、財市場の変動要素による「傾き」と「Y軸の切片」の変化を整理すると以下の通りとなります。
IS曲線の傾き
- 「限界消費性向(b)」の値が大きくなると傾きが緩やかになる
- 「投資の利子弾力性(I1)」の値が大きくなると傾きが緩やかになる
- 「限界輸入性向(m)」の値が大きくなると傾きが急になる
IS曲線のY軸の切片
- 「基礎消費(a)」の値が大きくなるとY軸の切片が大きくなる
- 「独立投資(I0)」の値が大きくなるとY軸の切片が大きくなる
- 「政府支出(G0)」の値が大きくなるとY軸の切片が大きくなる
- 「輸出(EX0)」の値が大きくなるとY軸の切片が大きくなる
- 「投資の利子弾力性(I1)」の値が大きくなるとY軸の切片が小さくなる
開放経済(税金(定額税)を考慮する場合)
「開放経済」において「総需要曲線(YD)」と「総供給曲線(YS)」を表す関数は以下の通りです。(C:消費、I:投資、G:政府支出、EX:輸出、IM:輸入、Y:GDP)
- YD = C + I + G + EX - IM
- YS = Y
「IS曲線」は「財市場」が均衡する点の組み合わせを表しているため「YD = YS」の関係が成立します。
- Y = C + I + G + EX - IM
「消費(C)」「投資(I)」「政府支出(G)」「輸出(EX)」「輸入(IM)」が以下の関数で与えられている場合
- C = a + b( Y - T0 )(a:基礎消費、b:限界消費性向、Y:GDP、T0:定額税)
- I = I0 - I1r(I0:独立投資、I1:投資の利子弾力性、r:利子率)
- G = G0(G0:政府支出)
- EX = EX0(EX0:輸出)
- IM = mY(m:限界輸入性向、Y:GDP)
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフである「IS曲線」を表す関数は以下の通りとなります。
- Y = a + b( Y - T0 )+ I0 - I1r + G0 + EX0 - mY
- I1r = -( 1 - b + m )Y +( a - bT0 + I0 + G0 + EX0 )
- r = -( 1 - b + m )÷ I1 × Y +( a - bT0 + I0 + G0 + EX0 )÷ I1

「IS曲線」を表す関数から、財市場の変動要素による「傾き」と「Y軸の切片」の変化を整理すると以下の通りとなります。
IS曲線の傾き
- 「限界消費性向(b)」の値が大きくなると傾きが緩やかになる
- 「投資の利子弾力性(I1)」の値が大きくなると傾きが緩やかになる
- 「限界輸入性向(m)」の値が大きくなると傾きが急になる
IS曲線のY軸の切片
- 「基礎消費(a)」の値が大きくなるとY軸の切片が大きくなる
- 「限界消費性向(b)」の値が大きくなるとY軸の切片が小さくなる
- 「定額税(T0)」の値が大きくなるとY軸の切片が小さくなる
- 「独立投資(I0)」の値が大きくなるとY軸の切片が大きくなる
- 「政府支出(G0)」の値が大きくなるとY軸の切片が大きくなる
- 「輸出(EX0)」の値が大きくなるとY軸の切片が大きくなる
- 「投資の利子弾力性(I1)」の値が大きくなるとY軸の切片が小さくなる
IS曲線の描写(簡便法)
「投資曲線」と「45度線図」を用いて「IS曲線」を描写していく方法ではなく、縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「IS曲線」を簡易に描写する方法について説明します。
「IS曲線」を簡易に描写する方法と言いながらも、「財政政策」などにより「IS曲線」がどのように変化するかを考える場合は、こちらの考え方を理解しておかないと付いていけなくなるため、非常に重要です。
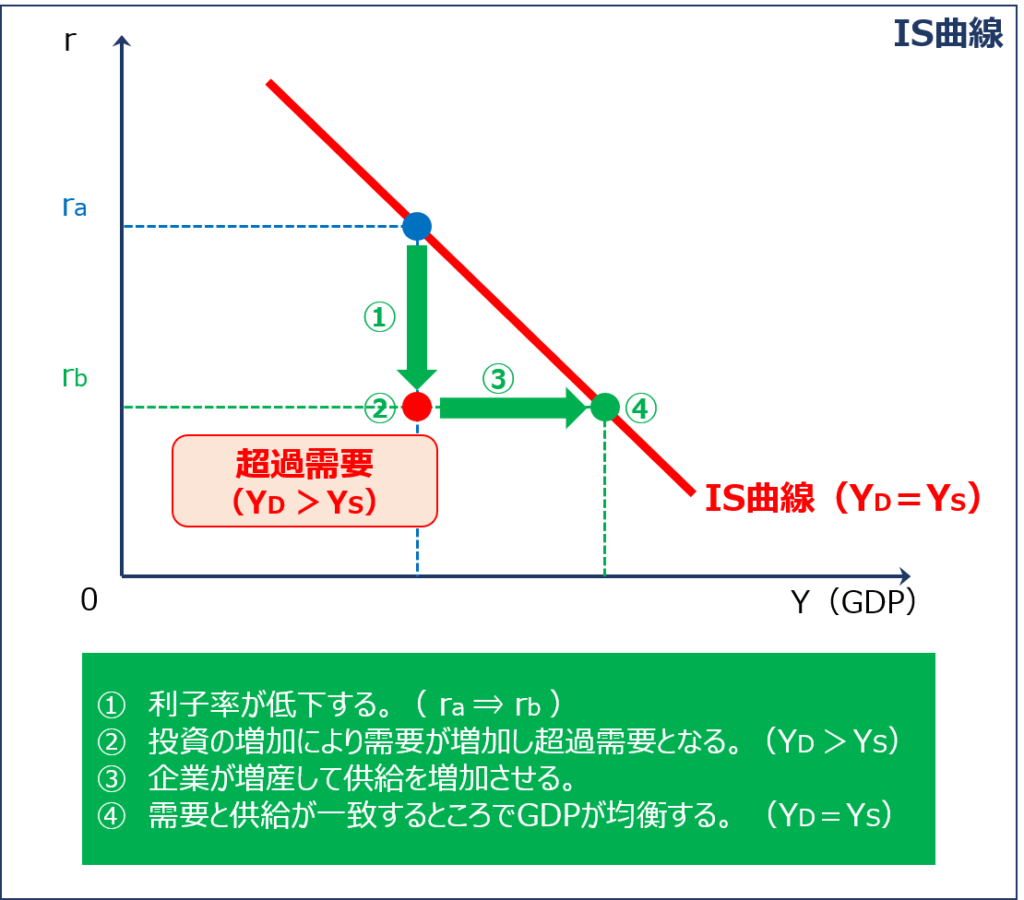
利子率が低下する場合
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「利子率(r)」が低下すると「均衡GDP(YE)」がどのように変化していくかを考えていきます。
- 「利子率(r)」が「ra」から「rb」に低下するため「ポイント(●)」はグラフの下側に移動する
- 「利子率(r)」の低下により「投資(I)」が増加するため「総需要(YD)」が増加して「財市場」が超過需要の状態(YD > YS)となる
- 「財市場」が超過需要の状態(YD > YS)になると企業が増産して「総供給(YS)」を増やすため「GDP(Y)」が高くなり「ポイント(●)」はグラフの右側に移動する
- 需要と供給が一致するところ(YD=YS)まで「GDP(Y)」が増加して「財市場」が均衡する
したがって、「利子率(r)」の低下により「ポイント(●)」はグラフの右下に移動するため「IS曲線」は右下がりの曲線として表されます。
利子率が低下する場合
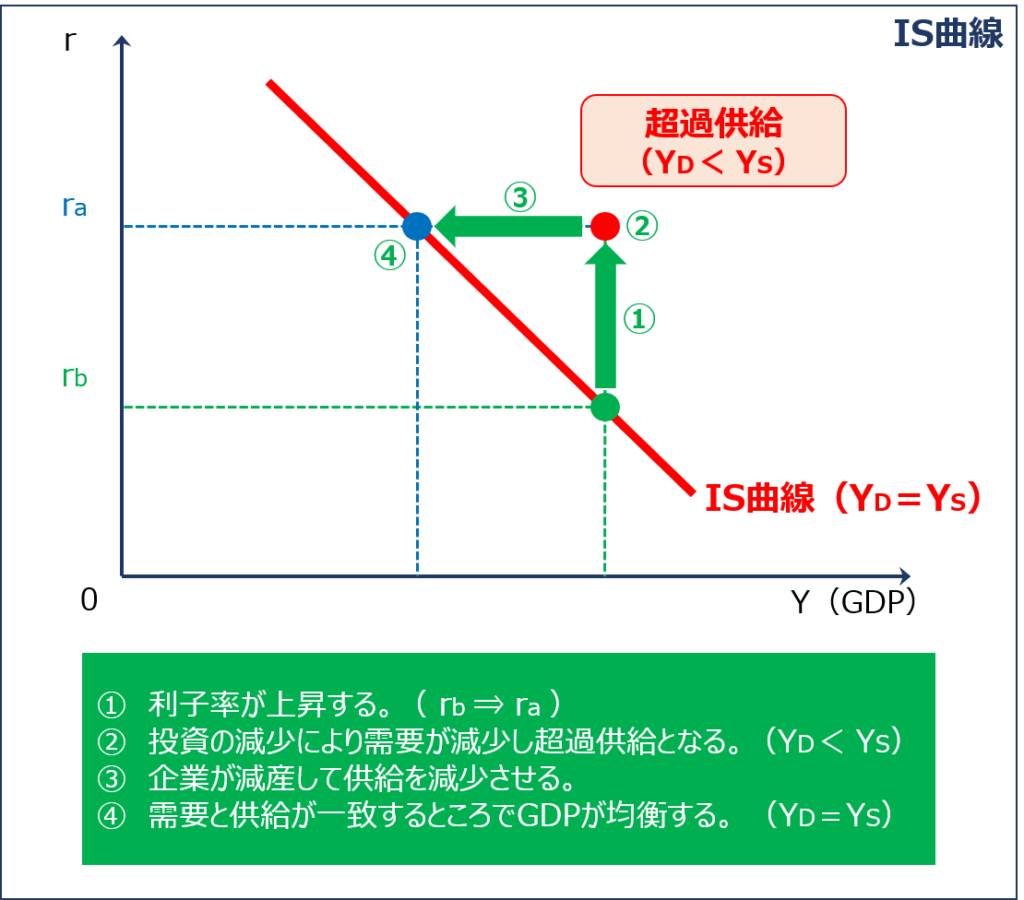
利子率が上昇する場合
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「利子率(r)」が上昇すると「均衡GDP(YE)」がどのように変化していくかを考えていきます。
- 「利子率(r)」が「rb」から「ra」に上昇するため「ポイント(●)」はグラフの上側に移動する
- 「利子率(r)」の上昇により「投資(I)」が減少するため「総需要(YD)」が減少して「財市場」が超過供給の状態(YD < YS)となる
- 「財市場」が超過供給の状態(YD < YS)になると企業が減産して「総供給(YS)」を減らすため「GDP(Y)」が低くなり「ポイント(●)」はグラフの左側に移動する
- 需要と供給が一致するところ(YD=YS)まで「GDP(Y)」が減少して「財市場」が均衡する
したがって、「利子率(r)」の上昇により「ポイント(●)」はグラフの左上に移動するため「IS曲線」は左上がり(右下がり)の曲線として表されます。
利子率が上昇する場合
LM曲線とは
「LM曲線」とは、縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「資本市場(貨幣市場)」が均衡する点の組み合わせを表す曲線のことをいいます。
「資本市場(貨幣市場)」において「GDP(Y)」が増加すると「利子率(r)」が上昇するため「LM曲線」は右上がりの曲線として表されます。
なお、「LM曲線」の「L」は「Liquidity Preference(流動性選好)」を、「M」は「Money Supply(貨幣供給)」を表しています。
LM曲線
LM曲線の描写
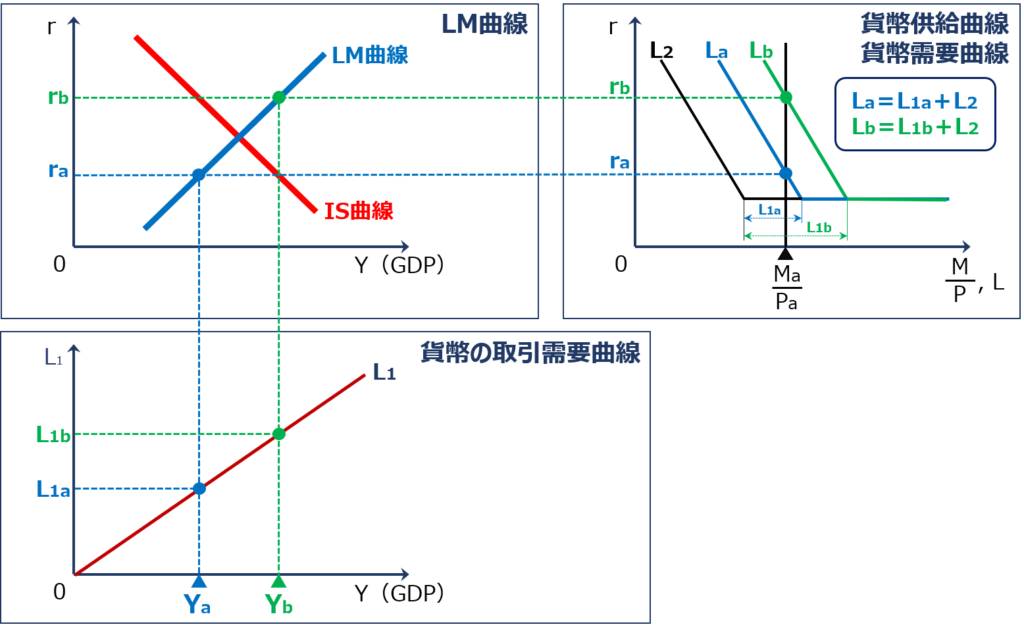
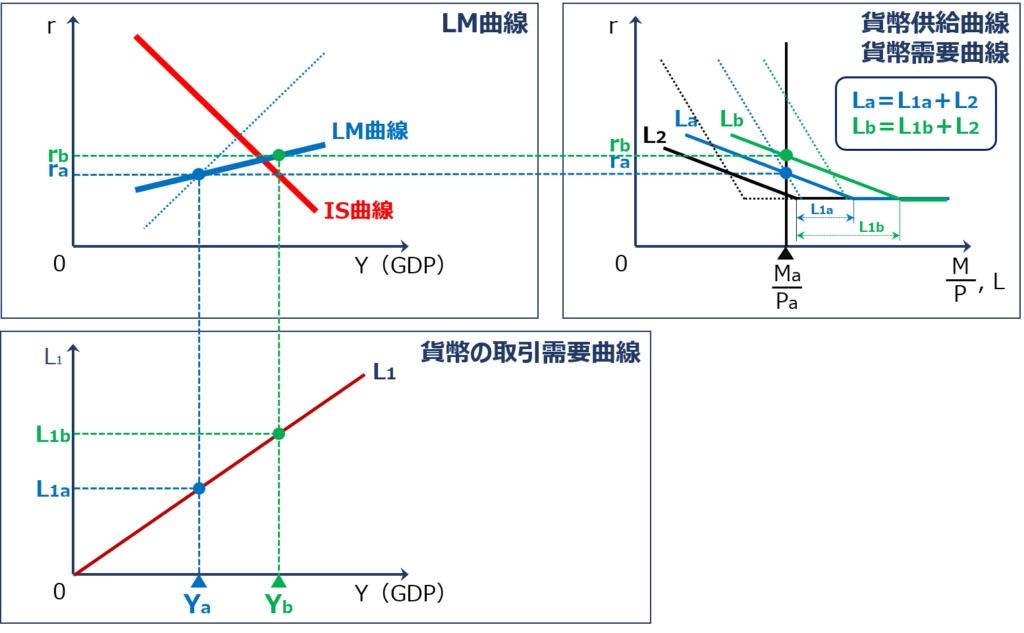
「LM曲線」は、縦軸に「利子率(r)」を、横軸に「実質貨幣供給量( M÷P )、貨幣需要量(L)」を取った「貨幣供給曲線/貨幣需要曲線」と、縦軸に「貨幣の取引需要(L1)」を、横軸に「GDP(Y)」を取った「貨幣の取引需要曲線」を用いて、「GDP(Y)」が変化したときに「利子率(r)」がどのように変化するかを確認していくことで描写することができます。
結論として、「GDP(Y)」が増加すると「利子率(r)」が上昇するため「LM曲線」は右上がりの曲線として表されます。
「GDP(Y)」が増加した場合に「利子率(r)」が変化していく流れを以下に示します。
- 「GDP(Y)」が「Ya」から「Yb」に増加する
- 「GDP(Y)」が増加したため「貨幣の取引需要(L1)」が「L1a」から「L1b」に増加する
- 「貨幣の取引需要(L1)」が増加したため「 L=L1+L2 」で表される「貨幣需要量(L)」が「La」から「Lb」に増加する
- 「貨幣需要量(L)」が増加したため「利子率(r)」が「ra」から「rb」に上昇する
- 「利子率(r)」が「ra」から「rb」に上昇したため「貨幣の資産需要(L2)」が減少して「資本市場(貨幣市場)」が均衡する
LM曲線の描写
貨幣の利子弾力性の大きさによるLM曲線の傾きの変化
「LM曲線」の傾きは「貨幣の利子弾力性」の大きさにより変化します。
「貨幣の利子弾力性」とは「利子率(r)」が変動したときに「貨幣の資産需要(L2)」がどれだけ反応するかを表しています。
「貨幣の利子弾力性」の大きさによる「LM曲線」の傾きの変化について説明するため、「貨幣需要曲線」から順に説明していきます。
貨幣需要曲線
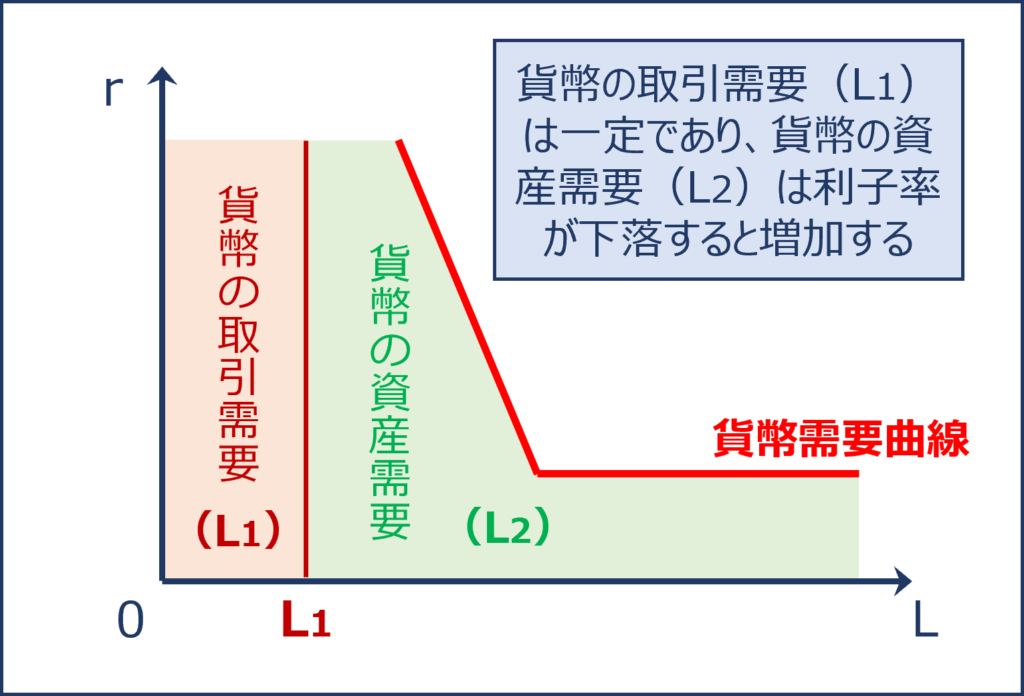
「貨幣需要(L)」は「GDP(Y)」の変動により増減する「貨幣の取引需要(L1)」と「利子率(r)」の変動により増減する「貨幣の資産需要(L2)」の合計として求められます。
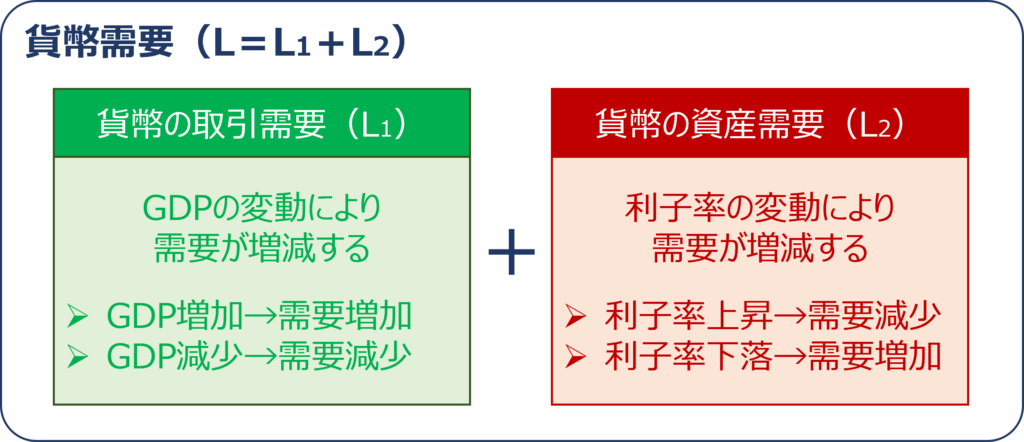
「利子率(r)」は「貨幣のレンタル価格」と表現されることが多く、「利子率(r)」が上昇(下落)すると「貨幣のレンタル価格」が上昇(下落)するため「貨幣の資産需要(L2)」が減少(増加)します。
「利子率(r)」が上昇したときに「貨幣の資産需要(L2)」が減少する流れを以下に示します。
- 「利子率(r)」が上昇すると「債券価格(PB)」が下落する
- 「債券価格(PB)」が下落すると「債券需要(DB)」が増加して「貨幣の資産需要(L2)」が減少する
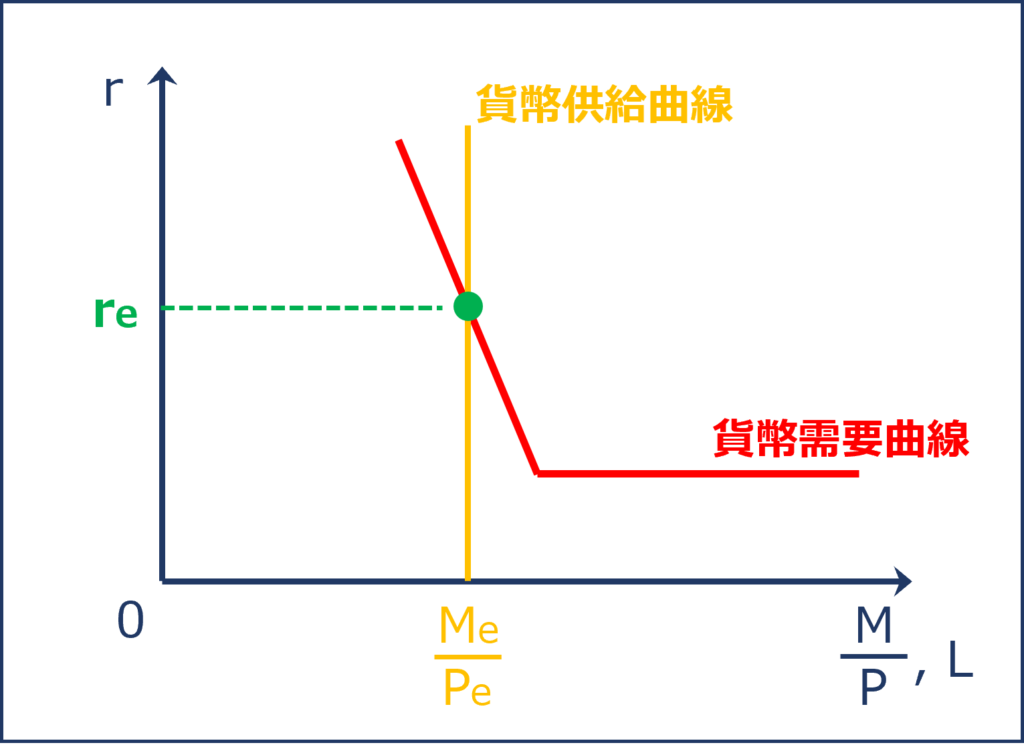
縦軸に「利子率(r)」を、横軸に「貨幣需要(L)」を取ったグラフに描画した「貨幣需要曲線」を以下に示します。
貨幣需要曲線
資本市場(貨幣市場)の均衡
「資本市場(貨幣市場)」では「貨幣の取引需要(L1)」と「貨幣の資産需要(L2)」の合計である「貨幣需要(L)」を表す「貨幣需要曲線」と「貨幣供給量(M÷P)」を表す「貨幣供給曲線」の交点で均衡して「利子率(r)」が「re」に決定します。
資本市場(貨幣市場)の均衡
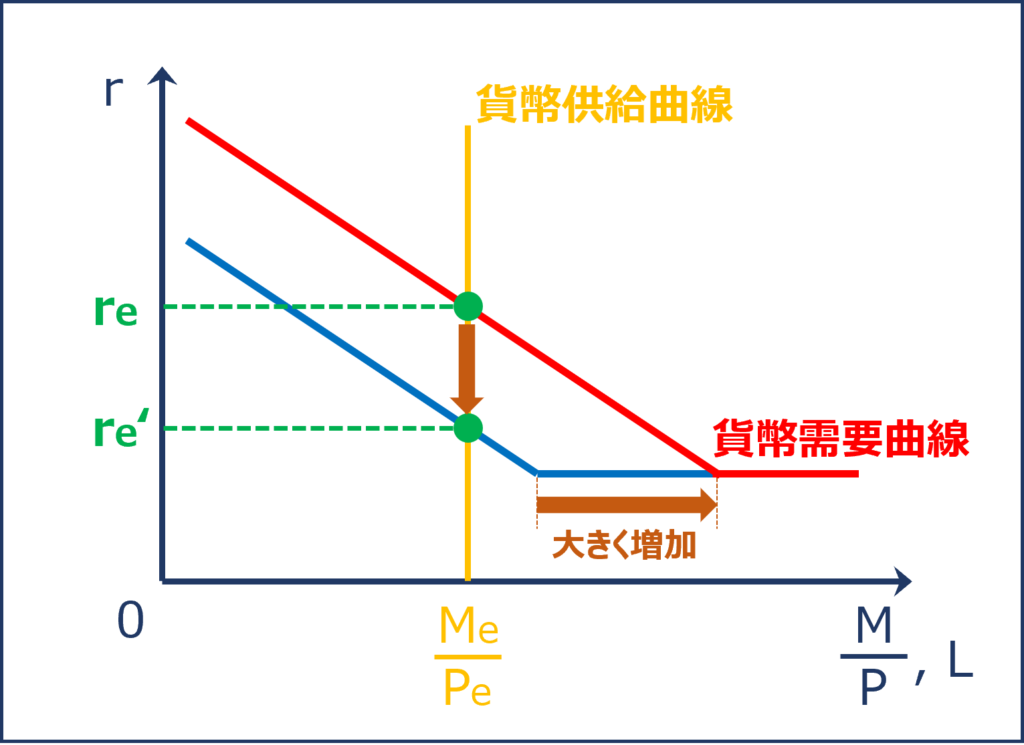
貨幣の利子弾力性の大きさによる貨幣需要曲線の傾きの変化
「貨幣の利子弾力性」が大きい場合、「利子率(r)」が下落(上昇)すると「貨幣の資産需要(L2)」が大きく増加(減少)して「貨幣需要(L)」も大きく増加(減少)します。
これは「貨幣需要曲線」が緩やかな傾きの曲線であることを表しています。
貨幣の利子弾力性が大きい場合
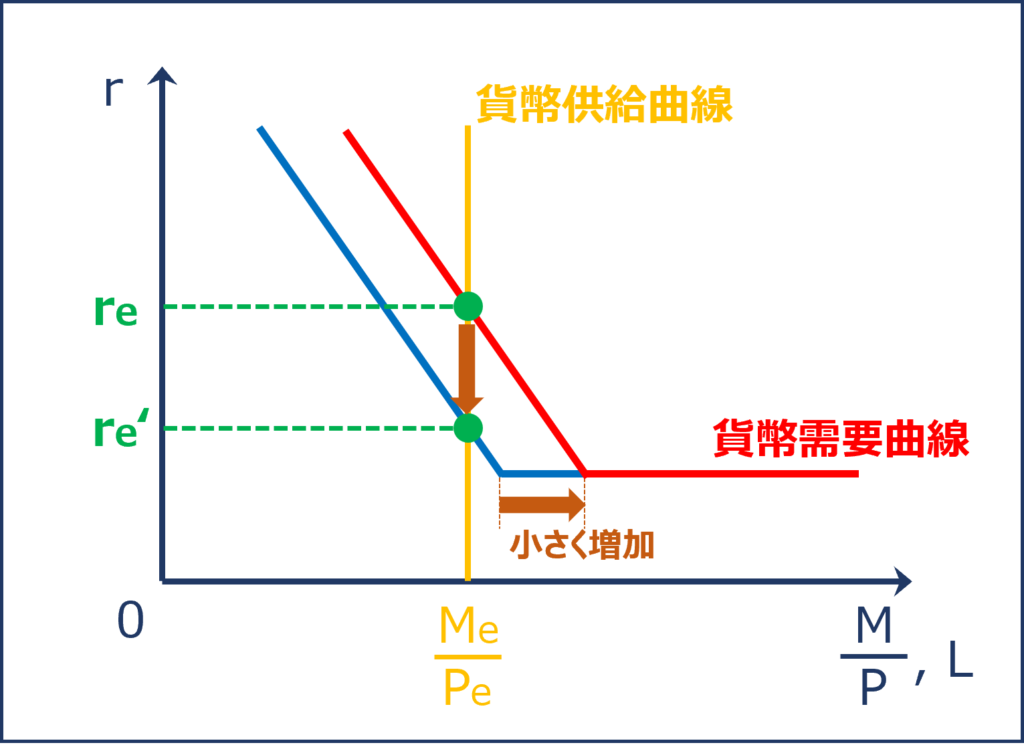
「貨幣の利子弾力性」が小さい場合、「利子率(r)」が下落(上昇)しても「貨幣の資産需要(L2)」が少ししか増加(減少)せず「貨幣需要(L)」も少ししか増加(減少)しません。
これは「貨幣需要曲線」が急な傾きの曲線であることを表しています。
貨幣の利子弾力性が小さい場合
「LM曲線」を考えるときのポイント
ここでは「利子率(r)」の変動による「貨幣需要(L)」の増減の大きさという流れで説明しましたが、「LM曲線」を考えるときには、この考え方(視点)が大きく変わってきます。(ここが「LM曲線」の分かりにくいところです)
「LM曲線」では「GDP(Y)」の増加(減少)により「貨幣の取引需要(L1)」が増加(減少)すると、「貨幣のレンタル価格」である「利子率(r)」が上昇(下落)して「貨幣の資産需要(L2)」が減少(増加)することによって「資本市場(貨幣市場)」が再び均衡しますが、「資本市場(貨幣市場)」が再び均衡するまでに上昇(下落)する「利子率(r)」の大きさが「貨幣の利子弾力性」の大きさによって異なってくるという視点で考える必要があります。
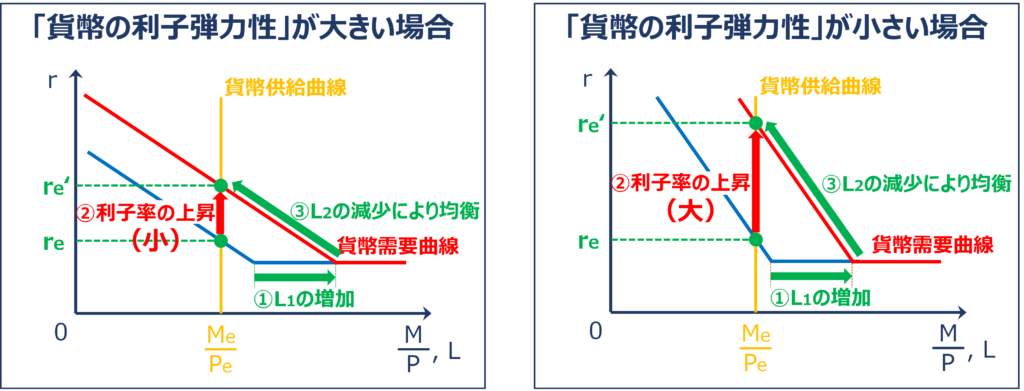
- 「貨幣の利子弾力性」が大きい場合
「資本市場(貨幣市場)」が均衡するまで「貨幣の資産需要(L2)」を減少(増加)させるために「利子率(r)」は少しだけ上昇(下落)すればよい - 「貨幣の利子弾力性」が小さい場合
「資本市場(貨幣市場)」が均衡するまで「貨幣の資産需要(L2)」を減少(増加)させるために「利子率(r)」は大きく上昇(下落)する必要がある
貨幣の利子弾力性の大きさによるLM曲線の傾きの変化
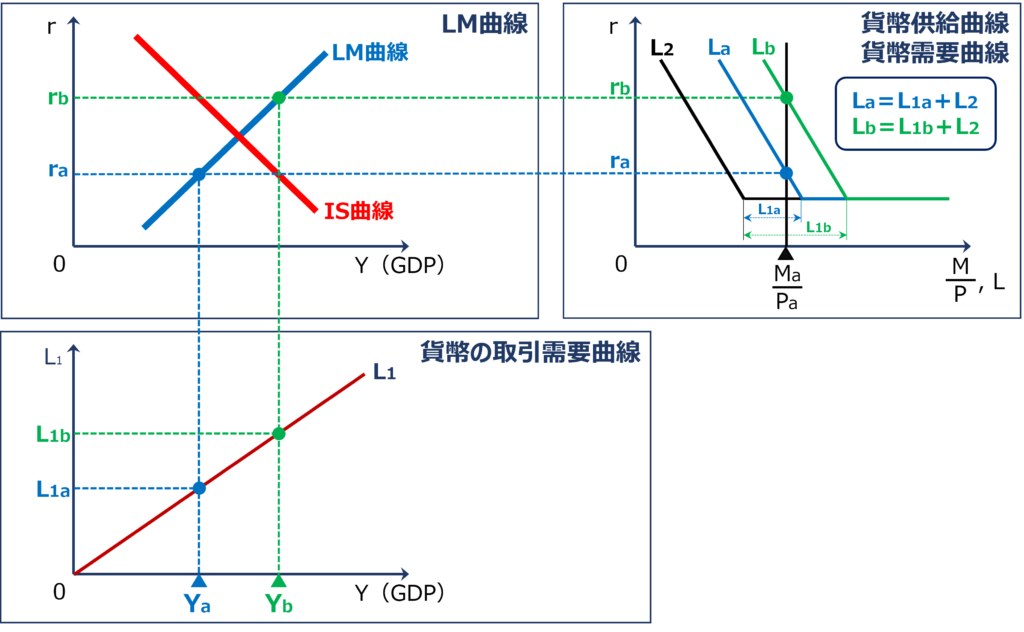
「LM曲線」では「GDP(Y)」の増加(減少)により「貨幣の取引需要(L1)」が増加(減少)すると、「貨幣のレンタル価格」である「利子率(r)」が上昇(下落)して「貨幣の資産需要(L2)」が減少(増加)することによって「資本市場(貨幣市場)」が再び均衡します。
「LM曲線」の傾きは、このときの「利子率(r)」の上昇(下落)の度合いにより変わってきます。
貨幣の利子弾力性が大きい場合
「貨幣の利子弾力性」が大きい場合、「利子率(r)」が少しだけ上昇(下落)すれば「資本市場(貨幣市場)」が均衡するまで「貨幣の資産需要(L2)」を減少(増加)させることができます。
そのため「投資の利子弾力性」が大きい場合は「LM曲線」の傾きは緩やかになります。
貨幣の利子弾力性が大きい場合
貨幣の利子弾力性が小さい場合
「貨幣の利子弾力性」が小さい場合、「利子率(r)」が大幅に上昇(下落)しなければ「資本市場(貨幣市場)」が均衡するまで「貨幣の資産需要(L2)」を減少(増加)させることはできません。
そのため「投資の利子弾力性」が小さい場合は「LM曲線」の傾きは急になります。
貨幣の利子弾力性が小さい場合
貨幣の利子弾力性がゼロの場合(貨幣が利子非弾力性な場合)
「貨幣の利子弾力性」がゼロの場合(貨幣が利子非弾力性な場合)「利子率(r)」が変動しても「貨幣の資産需要(L2)」が増減しなくなります。
そのため、「GDP(Y)」が増加(減少)して「貨幣の取引需要(L1)」が増加(減少)して「利子率(r)」が上昇(下落)しても「貨幣の資産需要(L2)」が減少(増加)しなくなるため「資本市場(貨幣市場)」が均衡するまで「貨幣の取引需要(L1)」が減少(増加)して元に戻ってしまい「GDP(Y)」も減少(増加)して元に戻ってしまいます。その結果、「LM曲線」は、垂直の曲線として表されます。
貨幣の利子弾力性がゼロの場合

貨幣の利子弾力性が無限大の場合(流動性のわな)
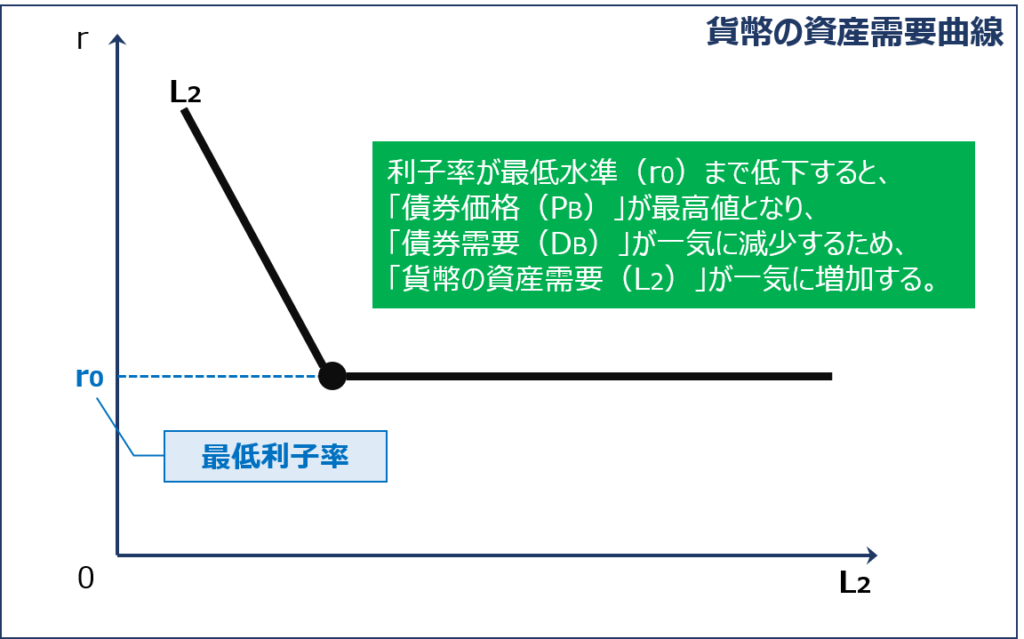
「貨幣の利子弾力性」が無限大になるケースとして「流動性のわな」があります。
「流動性のわな」とは「利子率(r)」が「最低水準(r0)」まで低下している状況のことをいい、このとき「貨幣の利子弾力性」は無限大になります。
具体的には、「利子率(r)」が「最低水準(r0)」まで低下すると、債券の価値が一気に高まり「債券価格(PB)」が最高水準になると同時に「債券需要(DB)」が一気に減少するため、結果として「貨幣の資産需要(L2)」が一気に増加するという状況が発生します。
貨幣の資産需要曲線
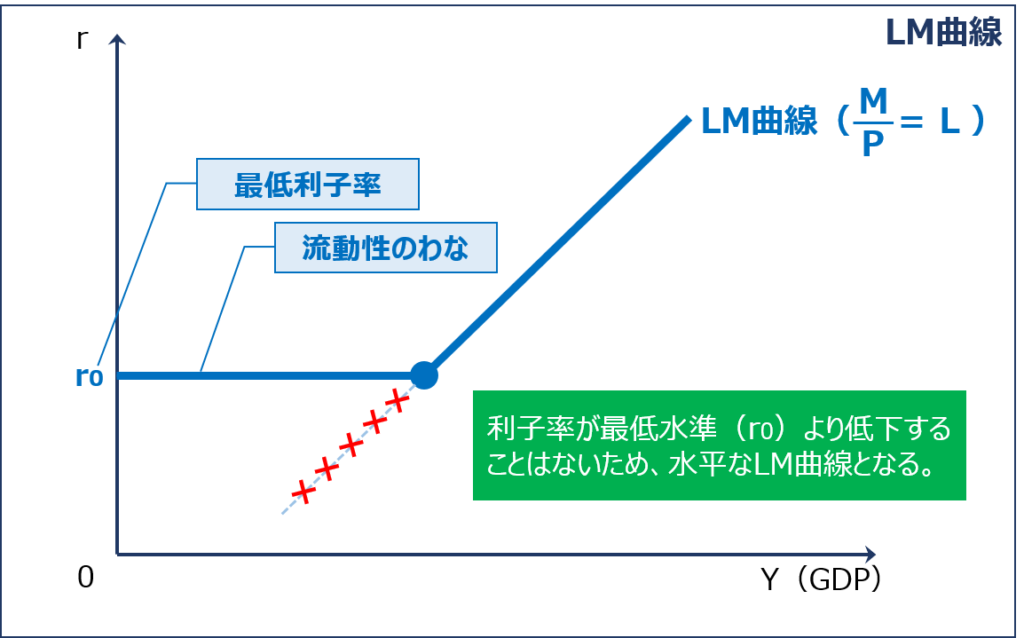
通常は、「GDP(Y)」が減少すると「貨幣の取引需要(L1)」が減少するため「利子率(r)」が下落しますが、「流動性のわな」の状況下においては「利子率(r)」が「最低水準(r0)」まで下落しているため「GDP(Y)」が減少して「貨幣の取引需要(L1)」が減少しても「利子率(r)」はそれ以上に下落しません。
その結果、「流動性のわな」の状況下においては「LM曲線」は「最低利子率(r0)」で水平となります。
LM曲線(流動性のわな)
LM曲線の描写(簡便法)
「貨幣供給曲線/貨幣需要曲線」と「貨幣の取引需要曲線」を用いて「LM曲線」を描写していく方法ではなく、縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「LM曲線」を簡易に描写する方法について説明します。
「LM曲線」を簡易に描写する方法と言いながらも、「金融政策」などにより「LM曲線」がどのように変化するかを考える場合は、こちらの考え方を理解しておかないと付いていけなくなるため、非常に重要です。
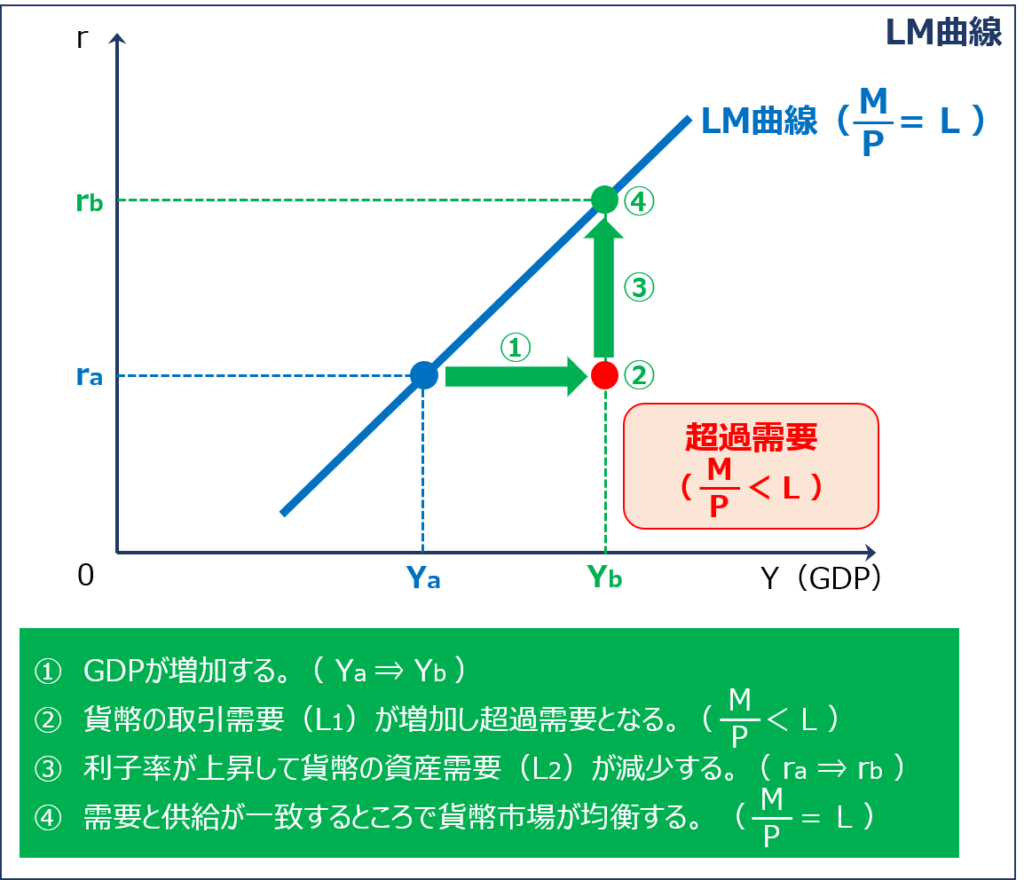
GDPが増加する場合
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「GDP(Y)」が増加すると「利子率(r)」がどのように変化していくかを考えていきます。
- 「GDP(Y)」が「Ya」から「Yb」に増加するため「ポイント(●)」はグラフの右側に移動する
- 「GDP(Y)」の増加により「資本市場(貨幣市場)」において「貨幣の取引需要(L1)」が増加するため「貨幣需要量( L = L1 + L2 )」が増加して「資本市場(貨幣市場)」が超過需要の状態( M÷P < L )となる
- 「資本市場(貨幣市場)」が超過需要の状態( M÷P < L )になると「利子率(r)」が「ra」から「rb」に上昇するため「ポイント(●)」はグラフの上側に移動する
- 「利子率(r)」が「ra」から「rb」に上昇すると「債券価格(PB)」が下降する
- 「債券価格(PB)」が下降すると「債券需要(DB)」が増加する
- 「債券需要(DB)」が増加すると「貨幣の資産需要(L2)」が減少する
- 需要と供給が一致するところ( M÷P = L )まで「貨幣の資産需要(L2)」が減少して「資本市場(貨幣市場)」が均衡する
したがって、「GDP(Y)」の増加により「ポイント(●)」はグラフの右上に移動するため「LM曲線」は右上がりの曲線として表されます。
GDPが増加する場合
GDPが減少する場合
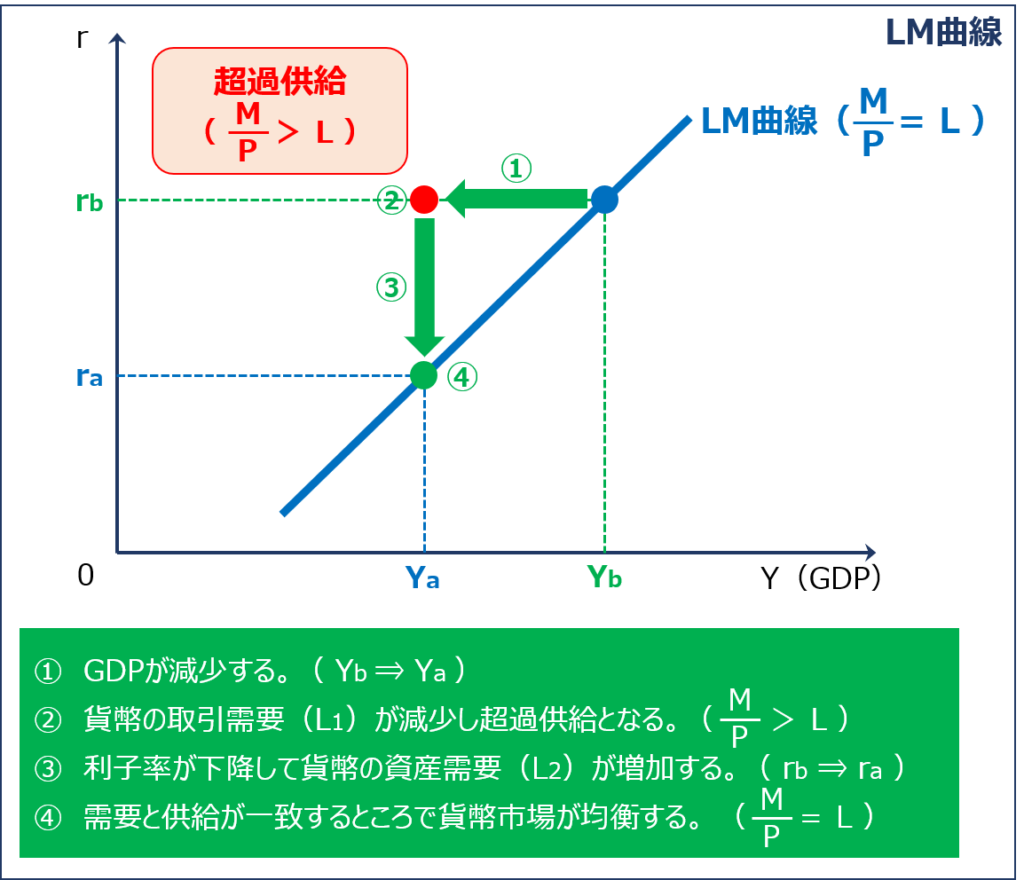
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフにおいて「GDP(Y)」が減少すると「利子率(r)」がどのように変化していくかを考えていきます。
- 「GDP(Y)」が「Yb」から「Ya」に減少するため「ポイント(●)」はグラフの左側に移動する
- 「GDP(Y)」の減少により「資本市場(貨幣市場)」において「貨幣の取引需要(L1)」が減少するため「貨幣需要量( L=L1+L2 )」が減少して「資本市場(貨幣市場)」が超過供給の状態( M÷P > L )となる
- 「資本市場(貨幣市場)」が超過供給の状態( M÷P > L )になると「利子率(r)」が「rb」から「ra」に下降するため「ポイント(●)」はグラフの下側に移動する
- 「利子率(r)」が「rb」から「ra」に下降すると「債券価格(PB)」が上昇する
- 「債券価格(PB)」が上昇すると「債券需要(DB)」が減少する
- 「債券需要(DB)」が減少すると「貨幣の資産需要(L2)」が増加する
- 需要と供給が一致するところ( M÷P = L )まで「貨幣の資産需要(L2)」が増加して「資本市場(貨幣市場)」が均衡する
したがって、「GDP(Y)」の減少により「ポイント(●)」はグラフの左下に移動するため「LM曲線」は左下がりの曲線(右上がりの曲線)として表されます。
GDPが減少する場合
試験問題
それでは、実際の試験問題を解いてみます。
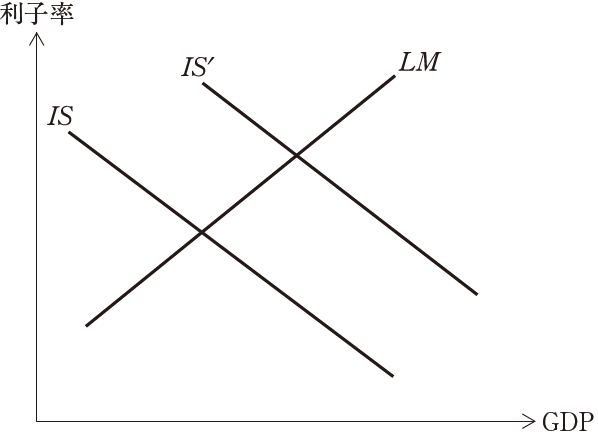
【平成28年度 第11問】
財政・金融政策の効果を理解するためには、IS-LM分析が便利である。IS曲線とLM曲線が下図のように描かれている。下記の設問に答えよ。
(設問1)
IS曲線とLM曲線の傾きに関する説明として、最も適切なものはどれか。
ア IS曲線は、限界消費性向が大きいほど、より緩やかに描かれる。
イ LM曲線は、貨幣の利子弾力性が小さいほど、より緩やかに描かれる。
ウ 利子率が高くなるほど貨幣需要が拡大すると考えており、したがってLM曲線は右上がりとなる。
エ 利子率が高くなるほど投資需要が拡大すると考えており、したがってIS曲線は右下がりとなる。
中小企業診断協会Webサイト(https://www.j-smeca.jp/contents/010_c_/shikenmondai.html)
考え方と解答(設問1)
「IS曲線」と「LM曲線」の傾きに関する知識を問う問題です。
(ア) 適切です。
試験問題において「総需要曲線」「消費(C)」「投資(I)」を表す関数が与えられていません。
「限界消費性向(b)」の変動により「IS曲線」の「傾き」がどのように変化するかを求められているため、最も簡単な「YD = C + I」から「IS曲線」を表す関数を求めていきます。
- YD = C + I(C:消費、I:投資)
- YS = Y(Y:GDP)
「IS曲線」は「財市場」が均衡する点の組み合わせを表しているため「YD = YS」の関係が成立します。
- Y = C + I
「消費(C)」「投資(I)」を表す関数を以下のようにした場合
- C = a + bY(a:基礎消費、b:限界消費性向、Y:GDP)
- I = I0 - I1r(I0:独立投資、I1:投資の利子弾力性、r:利子率)
縦軸に「利子率(r)」を、横軸に「GDP(Y)」を取ったグラフである「IS曲線」を表す関数は以下の通りとなります。
- Y = a + bY + I0 - I1r
- I1r = -( 1 - b )Y +( a + I0 )
- r = -( 1 - b )÷ I1 × Y +( a + I0 )÷ I1

「IS曲線」を表す関数から、財市場の変動要素による「傾き」と「Y軸の切片」の変化を整理すると以下の通りとなります。
IS曲線の傾き
- 「限界消費性向(b)」の値が大きくなると傾きが緩やかになる
- 「投資の利子弾力性(I1)」の値が大きくなると傾きが緩やかになる
IS曲線のY軸の切片
- 「基礎消費(a)」の値が大きくなるとY軸の切片が大きくなる
- 「独立投資(I0)」の値が大きくなるとY軸の切片が大きくなる
- 「投資の利子弾力性(I1)」の値が大きくなるとY軸の切片が小さくなる
したがって、IS曲線は、限界消費性向が大きいほど、より緩やかに描かれるため、選択肢の内容は適切です。
(イ) 不適切です。
「LM曲線」の傾きは「貨幣の利子弾力性」の大きさにより変化します。
「貨幣の利子弾力性」とは「利子率(r)」が変動したときに「貨幣の資産需要(L2)」がどれだけ反応するかを表しています。
貨幣の利子弾力性が大きい場合
「貨幣の利子弾力性」が大きい場合、「利子率(r)」が少しだけ上昇(下落)すれば「資本市場(貨幣市場)」が均衡するまで「貨幣の資産需要(L2)」を減少(増加)させることができます。
そのため「投資の利子弾力性」が大きい場合は「LM曲線」の傾きは緩やかになります。
貨幣の利子弾力性が大きい場合

貨幣の利子弾力性が小さい場合
「貨幣の利子弾力性」が小さい場合、「利子率(r)」が大幅に上昇(下落)しなければ「資本市場(貨幣市場)」が均衡するまで「貨幣の資産需要(L2)」を減少(増加)させることはできません。
そのため「投資の利子弾力性」が小さい場合は「LM曲線」の傾きは急になります。
貨幣の利子弾力性が小さい場合

したがって、LM曲線は、貨幣の利子弾力性が小さいほどではなく、貨幣の利子弾力性が大きいほど、より緩やかに描かれるため、選択肢の内容は不適切です。
(ウ) 不適切です。
「LM曲線」は「GDP(Y)」の増加により「貨幣需要量(L)」が増加して「利子率(r)」が上昇するため「右上がりの曲線」として表されます。
- 「GDP(Y)」が「Ya」から「Yb」に増加するため「ポイント(●)」はグラフの右側に移動する
- 「GDP(Y)」の増加により「資本市場(貨幣市場)」において「貨幣の取引需要(L1)」が増加するため「貨幣需要量( L = L1 + L2 )」が増加して「資本市場(貨幣市場)」が超過需要の状態( M÷P < L )となる
- 「資本市場(貨幣市場)」が超過需要の状態( M÷P < L )になると「利子率(r)」が「ra」から「rb」に上昇するため「ポイント(●)」はグラフの上側に移動する
- 「利子率(r)」が「ra」から「rb」に上昇すると「債券価格(PB)」が下降する
- 「債券価格(PB)」が下降すると「債券需要(DB)」が増加する
- 「債券需要(DB)」が増加すると「貨幣の資産需要(L2)」が減少する
- 需要と供給が一致するところ( M÷P = L )まで「貨幣の資産需要(L2)」が減少して「資本市場(貨幣市場)」が均衡する
したがって、「GDP(Y)」の増加により「ポイント(●)」はグラフの右上に移動するため「LM曲線」は右上がりの曲線として表されます。
GDPが増加する場合

利子率が高くなるほど貨幣需要が拡大するのではなく、GDPが高くなるほど貨幣需要が拡大して利子率が高くなると考えており、したがってLM曲線は右上がりとなるため、選択肢の内容は不適切です。
(エ) 不適切です。
「IS曲線」は「利子率(r)」の低下により「投資(I)」が増加して「GDP(Y)」が増加するため「右下がりの曲線」として表されます。
- 「利子率(r)」が「ra」から「rb」に低下するため「ポイント(●)」はグラフの下側に移動する
- 「利子率(r)」の低下により「投資(I)」が増加するため「総需要(YD)」が増加して「財市場」が超過需要の状態(YD > YS)となる
- 「財市場」が超過需要の状態(YD > YS)になると企業が増産して「総供給(YS)」を増やすため「GDP(Y)」が高くなり「ポイント(●)」はグラフの右側に移動する
- 需要と供給が一致するところ(YD=YS)まで「GDP(Y)」が増加して「財市場」が均衡する
利子率が低下する場合

利子率が高くなるほどではなく、利子率が低くなるほど投資需要が拡大すると考えており、したがってIS曲線は右下がりとなるため、選択肢の内容は不適切です。
答えは(ア)です。

コメント