今回は、「運営管理 ~R2-12 能力と負荷(1)線形計画法~」について説明します。
目次
運営管理 ~令和2年度一次試験問題一覧~
令和2年度の試験問題に関する解説は、以下のページを参照してください。
最適セールスミックス
「最適セールスミックス」とは、限られた経営資源で、企業の営業利益を最大にするために、販売(生産)する複数製品の最適な販売比率を求めることです。
「製品の最大生産可能数」「従業員による最大労働時間数」といった制約条件の中で、「1単位当たりの限界利益」が高い製品をできるだけ多く生産できるように各製品の生産数量を決めていくことで、営業利益を最大化することができます。
制約条件が2つの場合
制約条件が複数設定されている場合は、「線形計画法」を用いて利益が最大となる販売比率(製造費率)を求めていきます。
線形計画法
「線形計画法」は、「最適なセールスミックス」を求めるための手法であり「リニア・プログラミング(LP)」とも呼ばれることがあります。
ちなみに、「線形計画法」ではグラフを描いて利益が最大となる点を求めますが、グラフ上に描かれる関数式がすべて直線(線形)で表されるため「線形計画法」と呼ばれています。
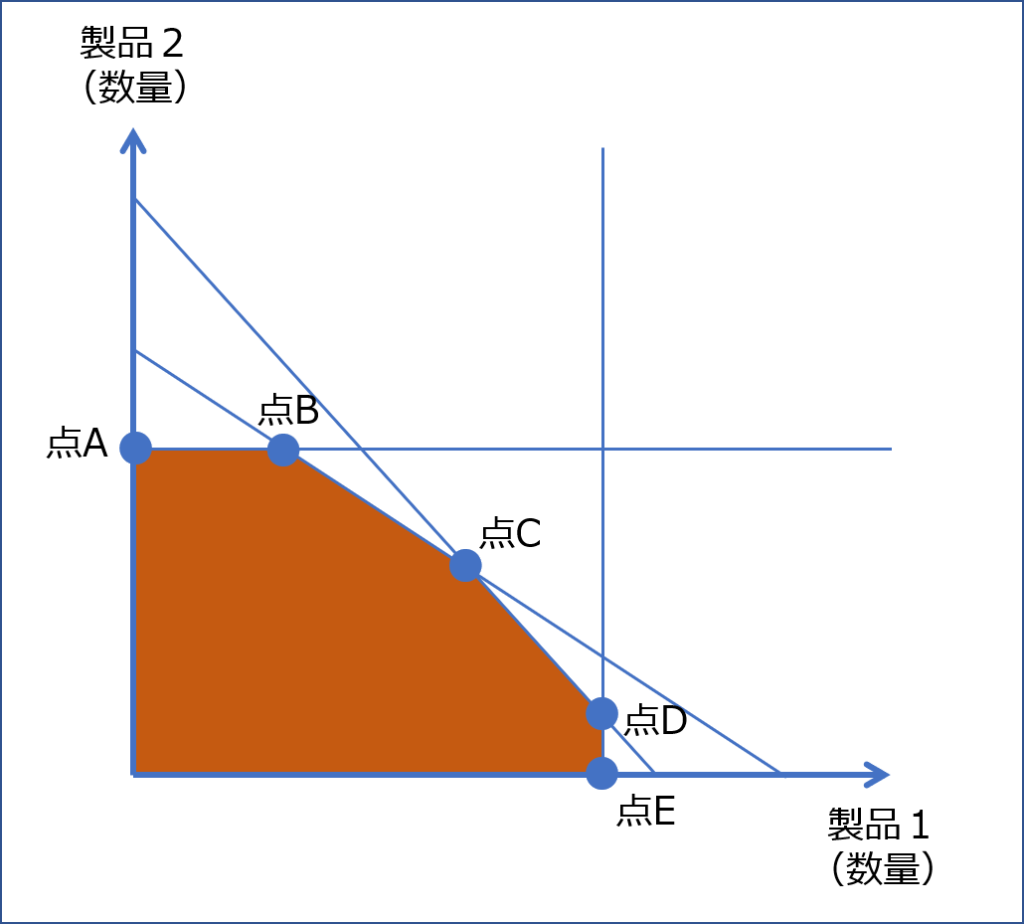
以下にグラフ(例)を示しますが、様々な制約条件を直線(線形)で示した場合に、それぞれの直線(線形)の交点である「点A~点E」のいずれかが利益を最大とする点となることを示しています。
「点A~点E」における利益をそれぞれ計算して、利益が最も大きくなる点の生産数量を「最適なセールスミックス」とします。
試験問題
それでは、実際の試験問題を解いてみます。
【令和2年度 第12問】
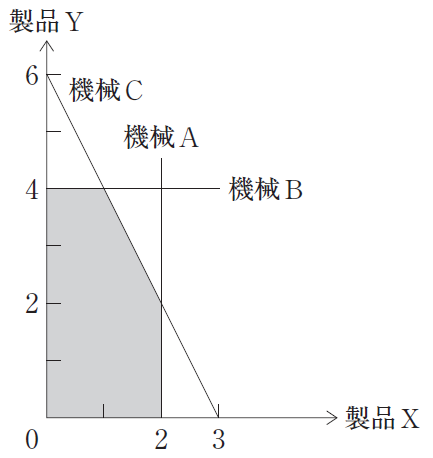
ある工場では、3台の機械を用いて2種類の製品X、Yの生産が可能である。下表には、製品を1単位生産するのに必要な各機械の工数と製品を1単位生産して得られる単位利益、および現状で使用可能な各機械の工数が示されている。また、下図は、下表に示した各機械における使用可能工数の制約を図示したものである。
総利益が最も高くなる方策として、最も適切なものを下記の解答群から選べ。
製品X 製品Y 使用可能工数 機械A 1 0 2 機械B 0 2 8 機械C 4 2 12 単位利益 3 5
[解答群]
ア 機械Aの使用可能工数を現状から4引き上げて6とする。
イ 機械Bの使用可能工数を現状から4引き上げて12とする。
ウ 機械Cの使用可能工数を現状から4引き上げて16とする。
エ 機械Bの使用可能工数を現状から2引き上げて10、機械Cの使用可能工数を現状から2引き上げて14とする。
中小企業診断協会Webサイト(https://www.j-smeca.jp/contents/010_c_/shikenmondai.html)
考え方と解答
「線形計画法」に関する知識を問う問題です。
「線形計画法」は、「最適なセールスミックス」を求めるための手法であり「リニア・プログラミング(LP)」とも呼ばれることがあります。
ちなみに、「線形計画法」ではグラフを描いて利益が最大となる点を求めますが、グラフ上に描かれる関数式がすべて直線(線形)で表されるため「線形計画法」と呼ばれています。
以下にグラフ(例)を示しますが、様々な制約条件を直線(線形)で示した場合に、それぞれの直線(線形)の交点である「点A~点E」のいずれかが利益を最大とする点となることを示しています。
「点A~点E」における利益をそれぞれ計算して、利益が最も大きくなる点の生産数量を「最適なセールスミックス」とします。

今回の問題では、全ての選択肢の条件を適用した場合に得られる総利益を算出しなければならないため、正解を導くためにはすごく時間がかかってしまいますが、「単位利益(限界利益)」の大きい製品の生産量を増やした方が「総利益」を効率的に増やすことができるため、「単位利益(限界利益)」が「3」である「製品X」の生産量を増やす方策よりも、「単位利益(限界利益)」が「5」である「製品Y」の生産量を増やす方策の方が、「総利益」を効率的に増やすことができることは覚えておきましょう。
選択肢(ア)
「機械A」の使用可能工数を現状から「4」引き上げて「6」とした場合、製品を1単位生産するのに必要な各機械の工数と製品を1単位生産して得られる単位利益、および現状で使用可能な各機械の工数の関係は以下の通りに変化します。
| 製品X | 製品Y | 使用可能工数 | |
| 機械A | 1 | 0 | 2 → 6 |
| 機械B | 0 | 2 | 8 |
| 機械C | 4 | 2 | 12 |
| 単位利益 | 3 | 5 |
上記の表に基づき、「機械A」「機械B」「機械C」において生産可能な「製品X」と「製品Y」の数量に関する制約を方程式として表します。
なお、「製品X」の生産数量を「X」とし、「製品Y」の生産数量を「Y」とします。
| 機械A | X ≦ 6 |
| 機械B | 2Y ≦ 8 Y ≦ 4 |
| 機械C | 4X+2Y ≦ 12 Y ≦ -2X+6 |
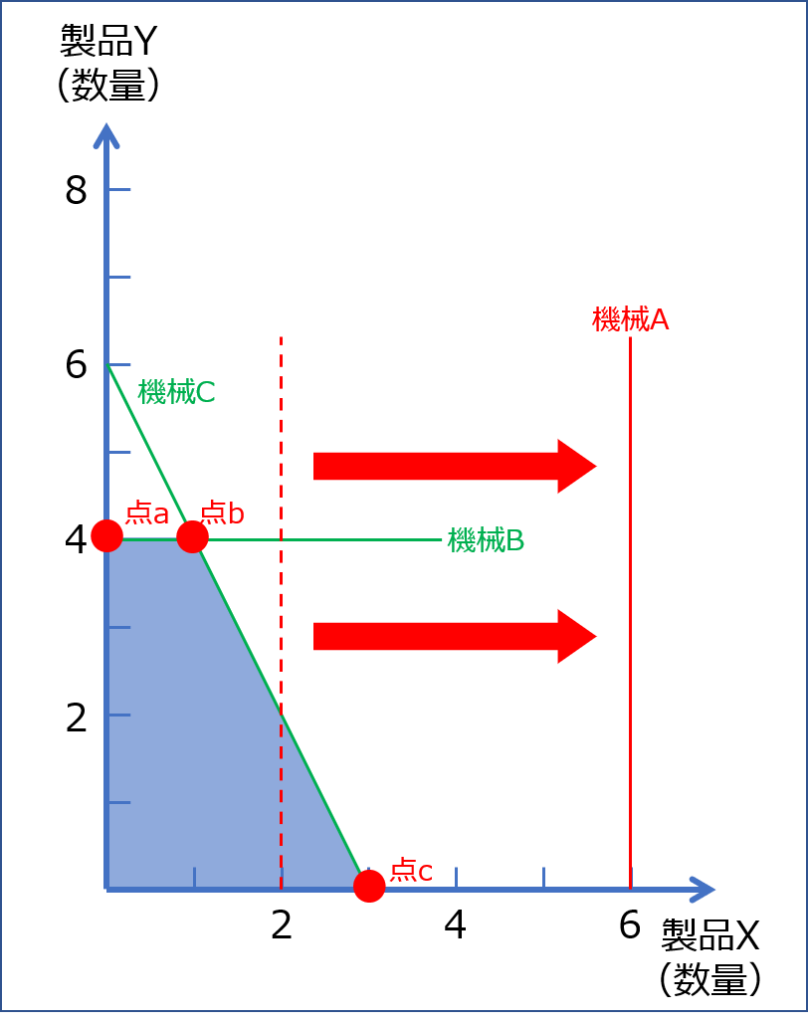
「機械A」「機械B」「機械C」における制約を示す方程式を以下に図示します。
総利益
それぞれの直線の交点である「点abc」のいずれかが、総利益を最大にする製品の最適な生産量の組み合わせであることを示しているため、「点abc」において得られる総利益を算出して比較します。
なお、総利益を算出するにあたって、「製品X」の単位利益を「α=3」とし、「製品Y」の単位利益を「β=5」とします。
- 点a :(X ,Y)=(0 ,4)= 4β = 4×5 = 20
- 点b :(X ,Y)=(1 ,4)= α+4β = 1×3+4×5 = 23
- 点c :(X ,Y)=(3 ,0)= 3α = 3×3 = 9
したがって、「機械A」の使用可能工数を現状から「4」引き上げて「6」としたときに、最大利益が得られる生産量の組み合わせは「点b(製品X=1/製品Y=4)」であり、その組み合わせにおける総利益は「23」です。
選択肢(イ)
「機械B」の使用可能工数を現状から「4」引き上げて「12」とした場合、製品を1単位生産するのに必要な各機械の工数と製品を1単位生産して得られる単位利益、および現状で使用可能な各機械の工数の関係は以下の通りに変化します。
| 製品X | 製品Y | 使用可能工数 | |
| 機械A | 1 | 0 | 2 |
| 機械B | 0 | 2 | 8 → 12 |
| 機械C | 4 | 2 | 12 |
| 単位利益 | 3 | 5 |
上記の表に基づき、「機械A」「機械B」「機械C」において生産可能な「製品X」と「製品Y」の数量に関する制約を方程式として表します。
なお、「製品X」の生産数量を「X」とし、「製品Y」の生産数量を「Y」とします。
| 機械A | X ≦ 2 |
| 機械B | 2Y ≦ 12 Y ≦ 6 |
| 機械C | 4X+2Y ≦ 12 Y ≦ -2X+6 |
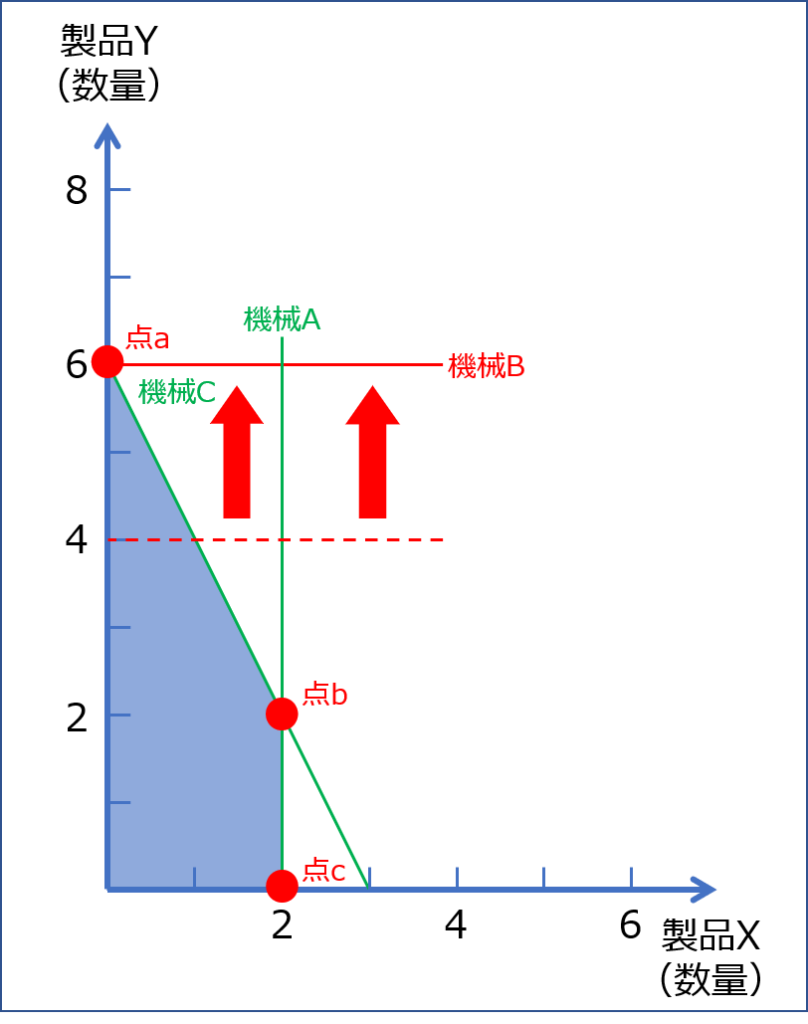
「機械A」「機械B」「機械C」における制約を示す方程式を以下に図示します。
総利益
それぞれの直線の交点である「点abc」のいずれかが、総利益を最大にする製品の最適な生産量の組み合わせであることを示しているため、「点abc」において得られる総利益を算出して比較します。
なお、総利益を算出するにあたって、「製品X」の単位利益を「α=3」とし、「製品Y」の単位利益を「β=5」とします。
- 点a :(X ,Y)=(0 ,6)= 6β = 6×5 = 30
- 点b :(X ,Y)=(2 ,2)= 2α+2β = 2×3+2×5 = 16
- 点c :(X ,Y)=(2 ,0)= 2α = 2×3 = 6
したがって、「機械B」の使用可能工数を現状から「4」引き上げて「12」としたときに、最大利益が得られる生産量の組み合わせは「点a(製品X=0/製品Y=6)」であり、その組み合わせにおける総利益は「30」です。
選択肢(ウ)
「機械C」の使用可能工数を現状から「4」引き上げて「16」とした場合、製品を1単位生産するのに必要な各機械の工数と製品を1単位生産して得られる単位利益、および現状で使用可能な各機械の工数の関係は以下の通りに変化します。
| 製品X | 製品Y | 使用可能工数 | |
| 機械A | 1 | 0 | 2 |
| 機械B | 0 | 2 | 8 |
| 機械C | 4 | 2 | 12 → 16 |
| 単位利益 | 3 | 5 |
上記の表に基づき、「機械A」「機械B」「機械C」において生産可能な「製品X」と「製品Y」の数量に関する制約を方程式として表します。
なお、「製品X」の生産数量を「X」とし、「製品Y」の生産数量を「Y」とします。
| 機械A | X ≦ 2 |
| 機械B | 2Y ≦ 8 Y ≦ 4 |
| 機械C | 4X+2Y ≦ 16 Y ≦ -2X+8 |
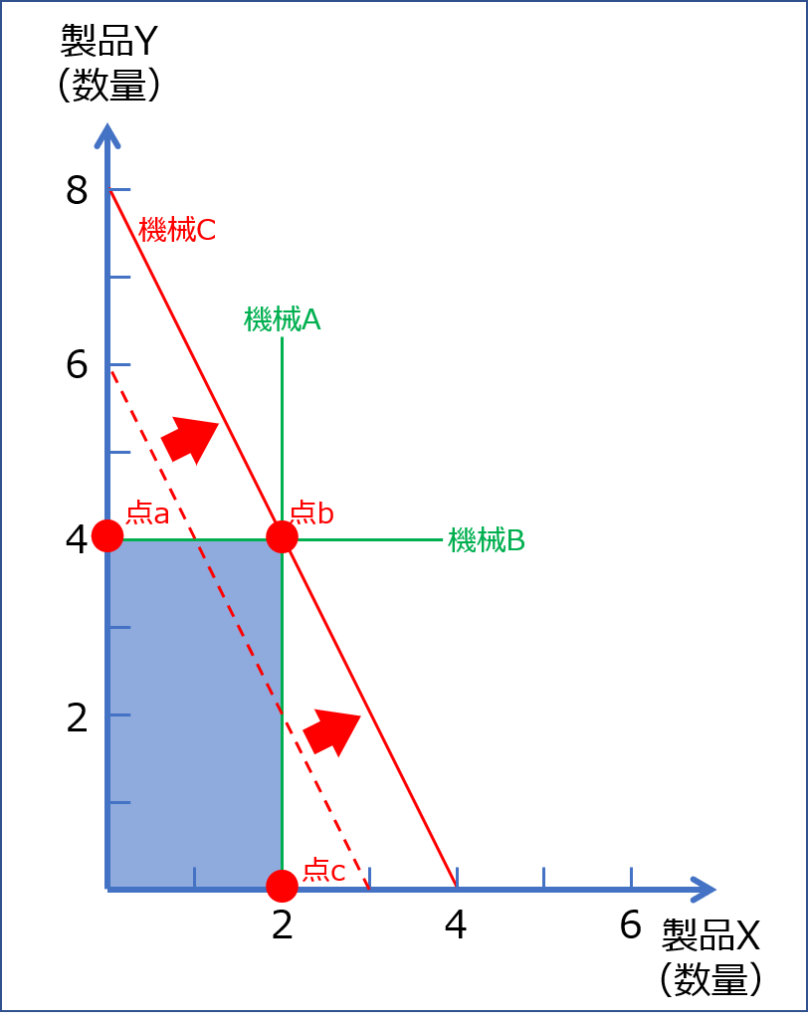
「機械A」「機械B」「機械C」における制約を示す方程式を以下に図示します。
総利益
それぞれの直線の交点である「点abc」のいずれかが、総利益を最大にする製品の最適な生産量の組み合わせであることを示しているため、「点abc」において得られる総利益を算出して比較します。
なお、総利益を算出するにあたって、「製品X」の単位利益を「α=3」とし、「製品Y」の単位利益を「β=5」とします。
- 点a :(X ,Y)=(0 ,4)= 4β = 4×5 = 20
- 点b :(X ,Y)=(2 ,4)= 2α+4β = 2×3+4×5 =26
- 点c :(X ,Y)=(2 ,0)= 2α = 2×3 = 6
したがって、「機械C」の使用可能工数を現状から「4」引き上げて「16」としたときに、最大利益が得られる生産量の組み合わせは「点b(製品X=2/製品Y=4)」であり、その組み合わせにおける総利益は「26」です。
選択肢(エ)
「機械B」の使用可能工数を現状から「2」引き上げて「10」、「機械C」の使用可能工数を現状から「2」引き上げて「14」とした場合、製品を1単位生産するのに必要な各機械の工数と製品を1単位生産して得られる単位利益、および現状で使用可能な各機械の工数の関係は以下の通りに変化します。
| 製品X | 製品Y | 使用可能工数 | |
| 機械A | 1 | 0 | 2 |
| 機械B | 0 | 2 | 8 → 10 |
| 機械C | 4 | 2 | 12 → 14 |
| 単位利益 | 3 | 5 |
上記の表に基づき、「機械A」「機械B」「機械C」において生産可能な「製品X」と「製品Y」の数量に関する制約を方程式として表します。
なお、「製品X」の生産数量を「X」とし、「製品Y」の生産数量を「Y」とします。
| 機械A | X ≦ 2 |
| 機械B | 2Y ≦ 10 Y ≦ 5 |
| 機械C | 4X+2Y ≦ 14 Y ≦ -2X+7 |
「機械A」「機械B」「機械C」における制約を示す方程式を以下に図示します。
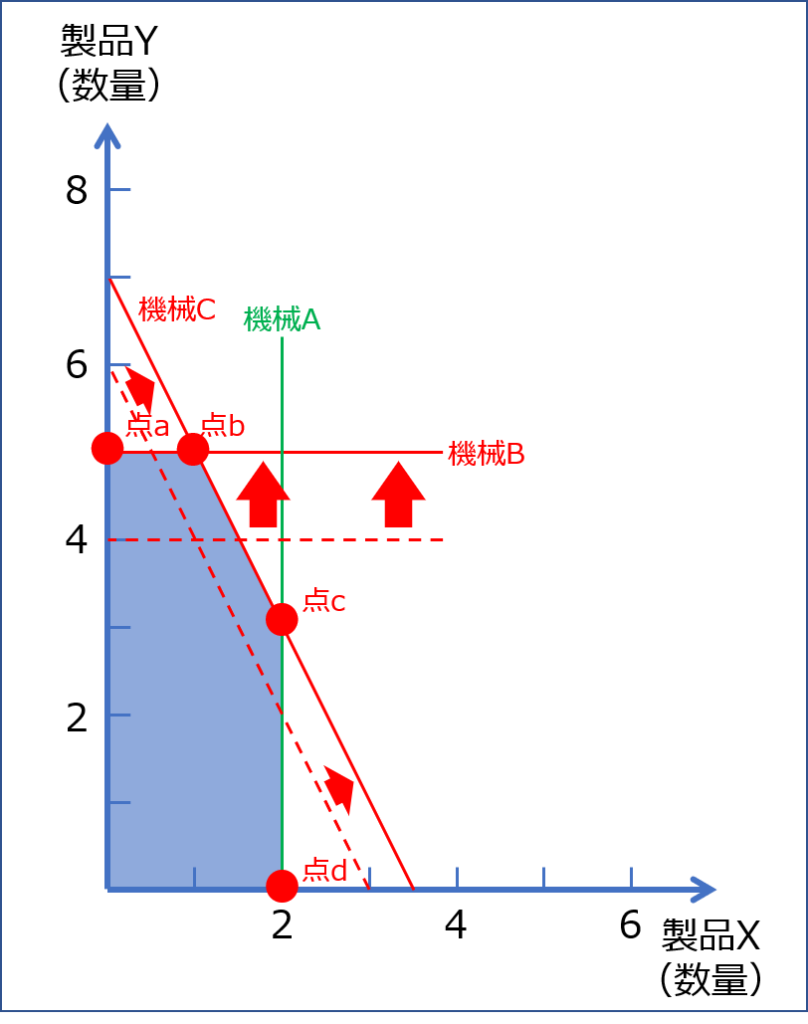
総利益
それぞれの直線の交点である「点abcd」のいずれかが、総利益を最大にする製品の最適な生産量の組み合わせであることを示しているため、「点abcd」において得られる総利益を算出して比較します。
なお、総利益を算出するにあたって、「製品X」の単位利益を「α=3」とし、「製品Y」の単位利益を「β=5」とします。
- 点a :(X ,Y)=(0 ,5 )= 5β = 5×5 = 25
- 点b :(X ,Y)=(1 ,5)= α+5β = 1×3+5×5 = 28
- 点c :(X ,Y)=(2 ,3)= 2α+3β = 2×3+3×5 = 21
- 点d :(X ,Y)=(2 ,0)= 2α = 2×3 = 6
したがって、「機械B」の使用可能工数を現状から「2」引き上げて「10」、「機械C」の使用可能工数を現状から「2」引き上げて「14」としたときに、最大利益が得られる生産量の組み合わせは「点b(製品X=1/製品Y=5)」であり、その組み合わせにおける総利益は「28」です。
総利益が最も高くなる方策
それぞれの条件において、最大利益が得られる生産量の組み合わせとその組み合わせで得られる総利益を以下に示します。
| 選択肢 | (X ,Y) | 総利益 |
| ア | (1 ,4) | 23 |
| イ | (0 ,6) | 30 |
| ウ | (2 ,4) | 26 |
| エ | (1 ,5) | 28 |
したがって、「選択肢(イ)」の方策を採用した場合が、最も総利益が高くなります。
答えは(イ)です。

コメント