今回は、「財務・会計 ~H30-13 社債の時間価値(2)~」について説明します。
二次試験の事例Ⅳで直接出題される論点ではありませんが、「時間価値(現在価値)」は当然に必要な知識として理解しておく必要があるため、一次試験の段階からしっかりと勉強しておきましょう。
目次
財務・会計 ~平成30年度一次試験問題一覧~
平成30年度の試験問題に関する解説は、以下のページを参照してください。
時間価値 -リンク-
一次試験に向けて「時間価値」について説明しているページを以下に示しますのでアクセスしてみてください。
貨幣の時間価値
社債の時間価値
割引現在価値
例えば、100万円の現金を10%の利息が付く銀行に預けると1年後には110万円になります。
つまり、10%の利息が付くことを前提に考えれば、1年後の110万円は、現時点の100万円と同じ価値であると考えることができます。
この場合、現時点での貨幣の価値(100万円)を「現在価値」、1年後の貨幣の価値(110万円)を「将来価値」といい、利息(10%)を「割引率」といいます。
ちなみに、100万円の現金を10%の利息が付く銀行に5年間預けると以下のようになります。

逆に、「将来価値」から「現在価値」を求める場合は以下のようになります。
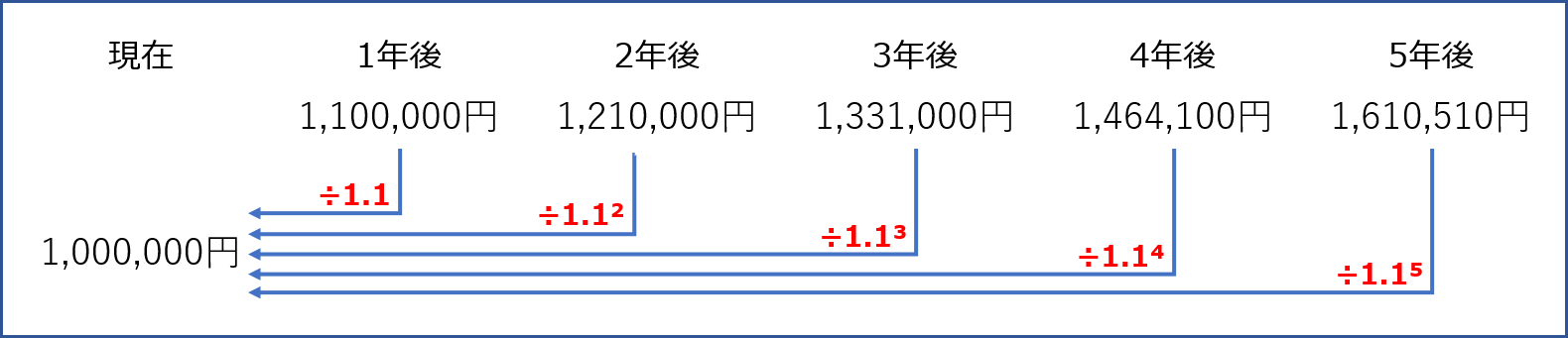
上記のように、「将来価値」を「割引率」で割り引いて求めた「現在価値」のことを「割引現在価値」といいます。
[例題1]
割引率が10%とした場合、5年後に手に入る「1,610,510円」の割引現在価値を求めよ。
[解答]
割引現在価値 = 1,610,510円÷1.1÷1.1÷1.1÷1.1÷1.1 = 1,000,000円
複利現価係数
「複利現価係数」とは「将来価値」から「現在価値」を求めるための係数です。
![]()
「複利現価係数」は、以下の計算式により算出することができます。

「割引率」が「10%」の場合の「複利現価係数」は以下の通りです。
- 1年:1÷1.1 = 0.9090…
- 2年:1÷1.1² = 0.8264…
- 3年:1÷1.1³ = 0.7513…
- 4年:1÷1.1⁴ = 0.6830…
- 5年:1÷1.1⁵ = 0.6209…
[例題2]
割引率が10%とした場合、複利現価係数を用いて5年後に手に入る「1,610,510円」の割引現在価値を求めよ。
| 1年後 | 2年後 | 3年後 | 4年後 | 5年後 | |
| 複利現価係数 | 0.9091 | 0.8264 | 0.7513 | 0.6830 | 0.6209 |
[解答]
割引現在価値 = 1,610,510円 × 0.6209 ≒ 999,966円(四捨五入)
(※)[例題1]と同じ金額を使った問題ですが、複利現価係数の小数点以下第5位以下が切り捨てられているので100万円にはなりません。
年金現価係数
「年金現価係数」とは、今後継続して一定の収入(支出)がある場合の収入総額(支出総額)の割引現在価値を求める係数です。

「割引率」が「10%」の場合の「年金現価係数」は以下の通りです。
- 1年:(1÷1.1) = 0.9090…
- 2年:(1÷1.1)+(1÷1.1²)= 1.7355…
- 3年:(1÷1.1)+(1÷1.1²)+(1÷1.1³)= 2.4868…
- 4年:(1÷1.1)+(1÷1.1²)+(1÷1.1³)+(1÷1.1⁴)= 3.1698…
- 5年:(1÷1.1)+(1÷1.1²)+(1÷1.1³)+(1÷1.1⁴)+(1÷1.1⁵)= 3.7907…
[例題3]
割引率が10%とした場合、今後5年間継続して「1,000,000円」を入手した場合の総収入額の割引現在価値を求めよ。
| 1年後 | 2年後 | 3年後 | 4年後 | 5年後 | |
| 年金現価係数 | 0.9091 | 1.7355 | 2.4868 | 3.1698 | 3.7907 |
[解答]
割引現在価値 = 1,000,000円 × 3.7907 = 3,790,700円
複利現価係数と年金現価係数を用いた割引現在価値の計算
[例題4]
1年後から3年後まで、毎年100万円ずつ収入が入る予定である。
割引率を3%とした場合、複利現価係数と年金現価係数を用いて総収入額の割引現在価値を求めよ。
【今後の収入予定】
| 1年後 | 2年後 | 3年後 | |
| 収入 | ¥1,000,000 | ¥1,000,000 | ¥1,000,000 |
【割引率を3%とした場合の複利現価係数と年金現価係数】
| 1年後 | 2年後 | 3年後 | |
| 複利現価係数 | 0.9709 | 0.9426 | 0.9151 |
| 年金現価係数 | 0.9709 | 1.9135 | 2.8286 |
[解答]
- 複利現価係数を利用した場合の算出方法
1,000,000円 × 0.9709 + 1,000,000円 × 0.9426 + 1,000,000円 × 0.9151 = 2,828,600円 - 年金現価係数を利用した場合の算出方法
1,000,000円 × 2.8286 = 2,828,600円
年金現価係数を用いた割引現在価値の計算
たまにパズルのような問題が出題されることもあります。
[例題5]
割引率が10%とした場合、年金現価係数を用いて5年後に手に入る「1,610,510円」の割引現在価値を求めよ。
| 1年後 | 2年後 | 3年後 | 4年後 | 5年後 | |
| 年金現価係数 | 0.9091 | 1.7355 | 2.4868 | 3.1698 | 3.7907 |
[解答]
割引現在価値 = 1,610,510円 × 3.7907 - 1,610,510円 × 3.1698 ≒ 999,966円
「貨幣の時間価値」は「設備投資の経済性計算」を解くにあたって、基本中の基本です。
「複利現価係数」と「年金現価係数」が与えられた場合は、その数値を用いて「割引現在価値」を計算しますが、「複利現価係数」と「年金現価係数」が与えられなかった場合は、電卓で「\1,000,000 ÷ 1.1 ÷ 1.1・・・」と計算していかなければなりません。
試験問題
それでは、実際の試験問題を解いてみます。
【平成30年度 第13問】
A社は、額面100万円の社債(償還までの期間が3年、クーポン・レート3%(年1回払い))を発行しようと考えている。現在、複利最終利回りは2.0%と予想される。このとき、A社の社債の価格はおよそいくらと考えられるか。最も適切なものを下記の解答群から選べ。なお、複利現価係数と年金現価係数は以下のものを使用すること。
複利現価係数 年金現価係数 期間(年) 2% 3% 2% 3% 1 0.980 0.971 0.980 0.971 2 0.961 0.943 1.941 1.914 3 0.942 0.915 2.883 2.829
[解答群]
ア 98万円
イ 100万円
ウ 103万円
エ 105万円
中小企業診断協会Webサイト(https://www.j-smeca.jp/contents/010_c_/shikenmondai.html)
考え方と解答
A社が発行しようと考えている、償還までの期間を3年に設定した額面100万円の社債の現時点における価格(割引現在価値)を求める問題です。
社債を発行するA社の視点から考えると、この社債にはクーポンレートが「3%」に設定されているため、毎年「3万円」の社債利息を支払うとともに、3年後に社債を償還するために100万円を支払う必要があります。
もちろん、社債を購入する出資者の視点から考えても大丈夫です。
社債を購入する出資者の視点から考えると、この社債にはクーポンレートが「3%」に設定されているため、毎年「3万円」の社債利息を受け取るとともに、3年後に社債が償還されるために100万円を受け取ることができます。
つまり、A社の社債は以下の2つの金額を合計することによって、その価格(割引現在価値)を算出することができます。
- 3年後に償還する金額(100万円)の割引現在価値
- 毎年支払う社債利息(3万円)の割引現在価値
割引率
将来の貨幣価値を、現時点の貨幣価値に換算するときに使用するものを割引率といい、今回の問題では複利最終利回り「2.0%」を「割引率」として、割引現在価値を算出していきます。
3年後に償還する金額(100万円)の割引現在価値
3年後に償還する金額「100万円」と割引率(複利最終利回り:2.0%)の複利現価係数(3年)「0.942」から、3年後に償還する金額(100万円)の割引現在価値を以下の通り求めることができます。
- 100万円 × 0.942 = 94.2万円
毎年支払う社債利息(3万円)の割引現在価値
毎年支払う社債利息「3万円」と割引率(複利最終利回り:2.0%)の年金現価係数(3年)「2.883」から、毎年支払う社債利息(3万円)の割引現在価値を以下の通り求めることができます。
- 3万円 × 2.883 = 8.649万円
社債の価格(割引現在価値)
3年後に償還する金額(100万円)の割引現在価値と毎年支払う社債利息(3万円)の割引現在価値を合計して、社債の価格(割引現在価値)をを以下の通り求めることができます。
- 94.2万円 + 8.649万円 = 102.849万円 ≒ 103万円
答えは(ウ)です。

コメント