運営管理 ～H29-27 商品構成（1）相乗積～

今回は、「運営管理 ～H29-27 商品構成（1）相乗積～」について説明します。

 

運営管理 ～平成29年度一次試験問題一覧～

平成29年度の試験問題に関する解説は、以下のページを参照してください。

• 運営管理 ～平成29年度一次試験問題一覧～

 

値入･粗利益･相乗積 －リンク－

本ブログにて「値入」「粗利益」「相乗積」について説明しているページを以下に示しますのでアクセスしてみてください。

 

• 値入･粗利益･相乗積のまとめ
• R5-28 商品構成（3）粗利益･相乗積
• R2-30 価格設定（7）価格決定手法
• R1-28 商品構成（2）相乗積
• H30-28 価格設定（1）価格決定手法
• H28-31 価格設定（3）価格決定手法
• H27-28 価格設定（4）価格決定手法
• H26-28 価格設定（6）価格決定手法

 

粗利益（粗利）

「粗利益（粗利）」とは「売上高」から「売上原価」を控除した「売上総利益」のことをいいます。

ここでは、小売業において個々の商品における粗利益（粗利）の考え方について簡易的に説明しています。

 

粗利益の算出

「粗利益」は「販売価格（売価）」から「仕入価格（原価）」を控除した金額であり、以下の公式により求めることができます。

 

 

粗利益率の算出

「粗利益率」とは「販売価格（売価）」に対する「粗利益」の割合であり、以下の公式により求めることができます。

 

 

 

仕入原価の算出

「仕入価格（原価）」は「販売価格（売価）」と「粗利益率」から以下の公式により求めることができます。

 

 

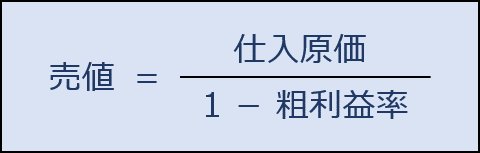
原価と粗利益率から売価を設定

「販売価格（売価）」は「仕入価格（原価）」と「粗利益率」から以下の公式により求めることができます。

 

 

 

相乗積

「相乗積」とは、２つ以上の数字を乗じて算出した積のことをいいます。

小売業の店舗においては、以下の計算式により求められる相乗積を活用して、商品別の利益貢献度を確認することができます。利益貢献度の高い商品の売上を増加させることができれば、店舗全体の利益率を効率的に高めることができます。

 

 

試験問題

それでは、実際の試験問題を解いてみます。

【平成29年度 第27問】

店舗Ｘにおける商品カテゴリー別の売上高と粗利高を示した次の表を見て、この店舗における今後の販売計画を検討する際の考え方に関する記述として最も適切なものを、下記の解答群から選べ。

ただし、値引きや廃棄ロスを考慮せず、商品カテゴリーごとの粗利益率は変動しないものとする。

 

商品カテゴリー	売上高	売上構成比	粗利高	粗利益率	相乗積
カテゴリーa	1,500万円	30.0%	600万円	40.0%	12.0%
カテゴリーb	1,000万円	20.0%	250万円	25.0%	5.0%
カテゴリーc	600万円	12.0%	300万円	50.0%	6.0%
カテゴリーd	1,200万円	24.0%	360万円	30.0%	7.2%
カテゴリーe	700万円	14.0%	315万円	45.0%	6.3%
全体	5,000万円	100.0%	1,825万円	36.5%

 

［解答群］

ア　カテゴリーbの売上高が表の数値の2倍になり、他のカテゴリーの売上高が変わらない場合、カテゴリーbの相乗積はカテゴリーaより高くなる。

イ　カテゴリーcの売上高が表の数値の2倍になり、他のカテゴリーの売上高が変わらない場合、カテゴリーcの相乗積は2倍になる。

ウ　カテゴリーeの売上高が表の数値の2倍になり、他のカテゴリーの売上高が変わらない場合、店舗全体の粗利益率は高まる。

エ　すべてのカテゴリーの売上高が表の数値からそれぞれ10％ずつ増えた場合、相乗積がもっとも増加するのはカテゴリーcである。

オ　すべてのカテゴリーの売上高が表の数値からそれぞれ100万円ずつ増えた場合、カテゴリーそれぞれの相乗積は変わらない。

 

中小企業診断協会Webサイト（https://www.j-smeca.jp/contents/010_c_/shikenmondai.html）

 

考え方と解答

店舗における「売上高」の増加に伴う「相乗積」や「店舗全体の粗利益率」の変動に関する問題です。

 

問題の本質は、「店舗全体の粗利益率よりも粗利益率が高い商品、つまり利益貢献度の高い商品の売上を増加させることができれば、店舗全体の粗利益率が増加する」ことを理解しているかということですが、検算のためにすべてのパターンを計算しようとすると、ある商品の売上高が増加した場合に、すべての商品の売上構成比が増減するため、計算が非常に面倒くさい問題です。

 

（ア） 不適切です。

「カテゴリーｂ」の売上高が表の数値の２倍になり、「他のカテゴリー」の売上高が変わらない場合、一覧の数値は以下の通りに変化します。

「カテゴリーｂ」の相乗積は「カテゴリーａ」よりも高くはならないため、選択肢の内容は不適切です。

 

商品カテゴリー	売上高	売上構成比	粗利高	粗利益率	相乗積
カテゴリーａ	1,500万円	25.0%	600万円	40.0%	10.0%
カテゴリーｂ	2,000万円	33.3%	500万円	25.0%	8.3%
カテゴリーｃ	600万円	10.0%	300万円	50.0%	5.0%
カテゴリーｄ	1,200万円	20.0%	360万円	30.0%	6.0%
カテゴリーｅ	700万円	11.7%	315万円	45.0%	5.3%
全体	6,000万円	100.0%	2,075万円	34.6%

 

（イ） 不適切です。

「カテゴリーｃ」の売上高が表の数値の２倍になり、「他のカテゴリー」の売上高が変わらない場合、一覧の数値は以下の通りに変化します。

「カテゴリーｃ」の相乗積は「6.0%→10.7%」に増加しますが「2倍」とはなっていないため、選択肢の内容は不適切です。

 

商品カテゴリー	売上高	売上構成比	粗利高	粗利益率	相乗積
カテゴリーａ	1,500万円	26.8%	600万円	40.0%	10.7%
カテゴリーｂ	1,000万円	17.9%	250万円	25.0%	4.5%
カテゴリーｃ	1,200万円	21.4%	600万円	50.0%	10.7%
カテゴリーｄ	1,200万円	21.4%	360万円	30.0%	6.4%
カテゴリーｅ	700万円	12.5%	315万円	45.0%	5.6%
全体	5,600万円	100.0%	2,125万円	37.9%

 

（ウ） 適切です。

「カテゴリーｅ」の売上高が表の数値の２倍になり、「他のカテゴリー」の売上高が変わらない場合、一覧の数値は以下の通りに変化します。

「店舗全体の粗利益率」が「36.5%→37.5%」に増加するため、選択肢の内容は適切です。

 

商品カテゴリー	売上高	売上構成比	粗利高	粗利益率	相乗積
カテゴリーａ	1,500万円	26.3%	600万円	40.0%	10.5%
カテゴリーｂ	1,000万円	17.5%	250万円	25.0%	4.4%
カテゴリーｃ	600万円	10.5%	300万円	50.0%	5.3%
カテゴリーｄ	1,200万円	21.1%	360万円	30.0%	6.3%
カテゴリーｅ	1,400万円	24.6%	630万円	45.0%	11.1%
全体	5,700万円	100.0%	2,140万円	37.5%

 

（エ） 不適切です。

「すべてのカテゴリー」の売上高が表の数値からそれぞれ10％ずつ増えた場合、一覧の数値は以下の通りに変化します。

すべての商品の売上高が一律に10%ずつ増えた場合は「売上構成比」が増減しないため、カテゴリーそれぞれの「相乗積」は変化しません。したがって、選択肢の内容は不適切です。

 

商品カテゴリー	売上高	売上構成比	粗利高	粗利益率	相乗積
カテゴリーａ	1,650万円	30.0%	660万円	40.0%	12.0%
カテゴリーｂ	1,100万円	20.0%	275万円	25.0%	5.0%
カテゴリーｃ	660万円	12.0%	330万円	50.0%	6.0%
カテゴリーｄ	1,320万円	24.0%	396万円	30.0%	7.2%
カテゴリーｅ	770万円	14.0%	347万円	45.0%	6.3%
全体	5,500万円	100.0%	2,008万円	36.5%

 

（オ） 不適切です。

「すべてのカテゴリー」の売上高が表の数値からそれぞれ100万円ずつ増えた場合、一覧の数値は以下の通りに変化します。

すべての商品の売上高が一律に100万円ずつずつ増えた場合は「売上構成比」が増減するため、カテゴリーそれぞれの「相乗積」も変動します。したがって、選択肢の内容は不適切です。

 

商品カテゴリー	売上高	売上構成比	粗利高	粗利益率	相乗積
カテゴリーａ	1,600万円	29.1%	640万円	40.0%	11.6%
カテゴリーｂ	1,100万円	20.0%	275万円	25.0%	5.0%
カテゴリーｃ	700万円	12.7%	350万円	50.0%	6.4%
カテゴリーｄ	1,300万円	23.6%	390万円	30.0%	7.1%
カテゴリーｅ	800万円	14.5%	360万円	45.0%	6.5%
全体	5,500万円	100.0%	2,015万円	36.6%

 

答えは（ウ）です。

---