今回は、「運営管理 ~R2-11 日程計画(6)PERT~」について説明します。
目次
運営管理 ~令和2年度一次試験問題一覧~
令和2年度の試験問題に関する解説は、以下のページを参照してください。
日程計画 -リンク-
本ブログにて、日程計画の「PERT」について説明しているページを以下に示しますのでアクセスしてみてください。
PERT(Program Evaluation and Review Technique)
「PERT」とは、順序関係が存在する複数の作業(アクティビティ)で構成されるプロジェクトを効率的に完了するためのスケジューリング手法です。
「PERT」では、プロジェクトの日程計画を「丸」と「矢印」で構成される「アローダイヤグラム」で表して、プロジェクト全体を完了させるために必要な最短の期間を算出していきます。
「アローダイヤグラム」は「○(ノード・結合点・イベント)」と「→(アクティビティ)」で構成されます。
試験問題
それでは、実際の試験問題を解いてみます。
【令和2年度 第11問】
下表は、あるプロジェクト業務を行う際の各作業の要件を示している。CPM(Critical Path Method)を適用して、最短プロジェクト遂行期間となる条件を達成したときの最小費用として、最も適切なものを下記の解答群から選べ(単位:万円)。
作業名 先行作業 所要期間 最短所要期間 単位時間当たりの短縮費用(万円) A - 5 4 10 B A 6 2 50 C B 7 3 90 D A 9 7 30 E C ,D 5 3 40
[解答群]
ア 440
イ 510
ウ 530
エ 610
オ 710
中小企業診断協会Webサイト(https://www.j-smeca.jp/contents/010_c_/shikenmondai.html)
考え方と解答
アローダイヤグラムの作成に関する知識を問う問題です。
アローダイヤグラムを作成してクリティカルパスを特定した後、クリティカルパス経路上にない作業の作業期間を、最短所要期間ではなく余裕期間を加味した作業期間に設定することで、作業時間の短縮にかかる費用を最小化していくという流れで考えていきます。
クリティカルパスの特定
アローダイヤグラムを作成してクリティカルパスを特定します。
アローダイヤグラムの作成
「アローダイヤグラム」は理解しているつもりでも、実際に作ってみると思った以上に難しくて作れなかったりすることもあるので、今回のプロジェクトに関する「アローダイヤグラム」を一から順に作成しながら説明していきます。
作業の相関図を作成する
複雑なプロジェクトにおいて、いきなり「アローダイヤグラム」を作成することは難しいため、まずは各作業の順序関係を把握するために相関図を作成します。
問題文で与えられた「アクティビティ(作業)」の前後関係を書き出すと以下の通りとなります。
- 「作業B,D」は「作業A」が完了してから着手します。
- 「作業C」は「作業B」が完了してから着手します。
- 「作業E」は「作業C,D」が完了してから着手します。
これらの前後関係に基づき、このプロジェクトにおける各作業の相関図を作成します。
この時点では「○」が「アクティビティ(作業)」となっていることに注意してください。
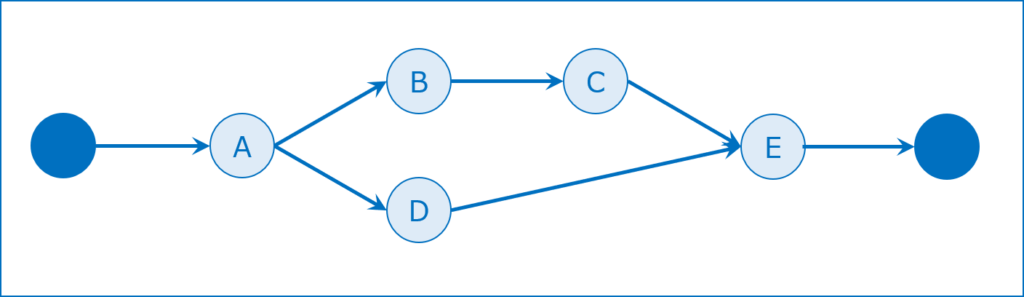
各作業を「○」から「→」に移動する
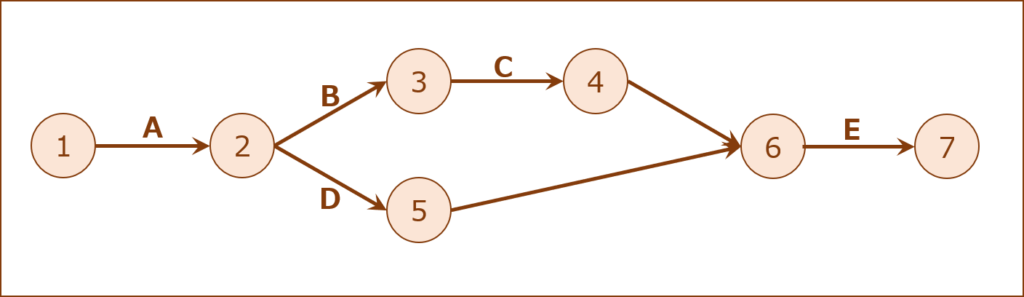
「アローダイヤグラム」に変換するために、作業の相関図において「○」で表現した「アクティビティ(作業)」を「→」に置き換えていきます。
先行作業が一つである「アクティビティ(作業)」の場合は左の「→」に、先行作業が複数である「アクティビティ(作業)」の場合は右の「→」に移動します。
このプロジェクトでは「作業E」は右の「→」に移動して、それ以外の作業は左の「→」に移動します。
この時点で「→」は「アクティビティ(作業)」を「○」は「ノード」を表すように変換されます。
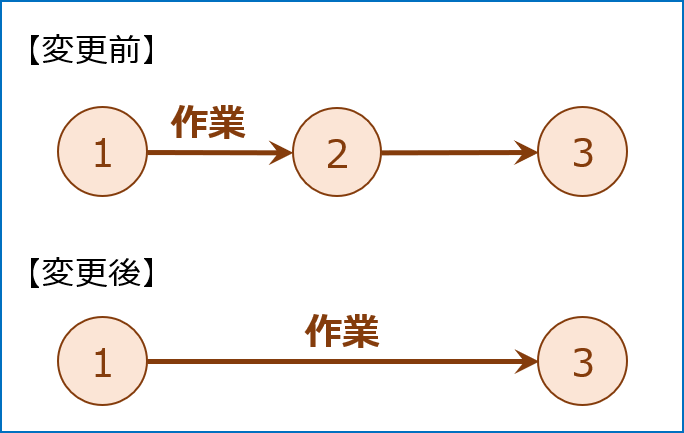
不要な「○(ノード)」を削除する
以下の構成となっている「○(ノード)」は不要なため、削除していきます。
今回のプロジェクトでは、以下の「○」を削除することができます。
- 「ノード3」⇒「作業C」⇒「ノード4」⇒「 」⇒「ノード6」
- 「ノード2」⇒「作業D」⇒「ノード5」⇒「 」⇒「ノード6」
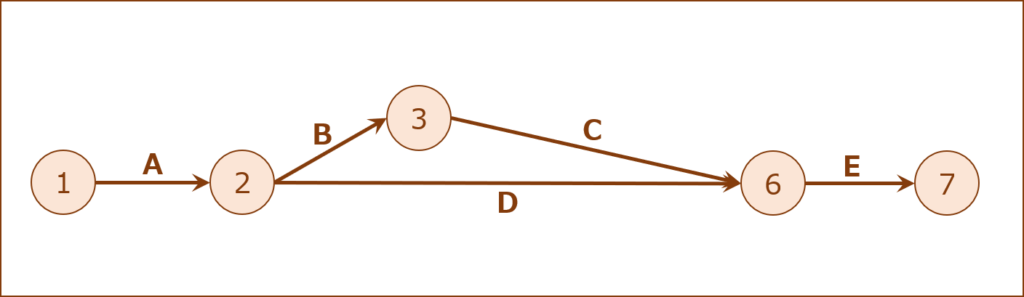
ダミー作業を特定する。
作業が割り当てられていない直線が「ダミー作業」です。
今回のプロジェクトでは「ダミー作業」はありません。
「ダミー作業」を使った「アローダイヤグラム」の作成については、過去に説明していますので、時間がある方は、以下のページも併せて確認してみてください。
形がいびつになったので、並び替えて「○」の番号を順番通りに書き換えます。
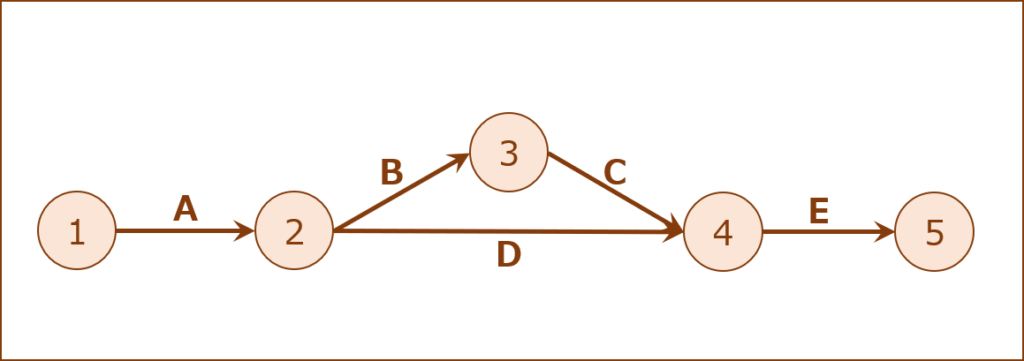
ダミー作業
「ダミー作業」は「アクティビティ(作業)」の順序関係を表示するために必要なものであり「作業期間:0」としてカウントされる「アクティビティ(作業)」のことをいいます。
EPSTとLPSTを追加する。
上記の図に「アクティビティ(作業)」の作業日数を追記して、「EPST(最早着手日)」と「LPST(最遅着手日)」の情報を追加していきます。
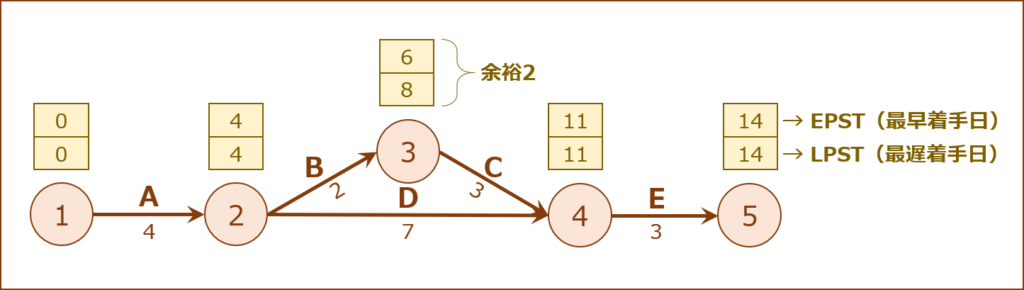
EPST(最早着手日)
「EPST(最早着手日)」とは「アクティビティ(作業)」に最も早く開始できる日を表しています。
例えば、プロジェクトの開始日から「ノード4」に到達するには「A→B→C:9日」の経路と「A→D:11日」の2つの経路がありますが、「E」を実行するには「C,D」の「アクティビティ(作業)」を完了しておく必要があるため「E」に着手できる「EPST(最早着手日)」は「11日」となります。
LPST(最遅着手日)
「LPST(最遅着手日)」とは「アクティビティ(作業)」に最も遅く着手できる日のことであり、プロジェクトを最短で終了させるために、少なくともこの日までに作業着手しなければならない日を表しています。
例えば、プロジェクトの終了日から逆算して「ノード2」に到達するには「E→D:10日」の経路と「E→C→B:8日」の2つの経路がありますが、終了日までにプロジェクトを完了させるためには遅くとも「10日前」までに「D」の「アクティビティ(作業)」に着手する必要があるため「ノード2」の「LPST(最遅着手日)」は「4日」となります。
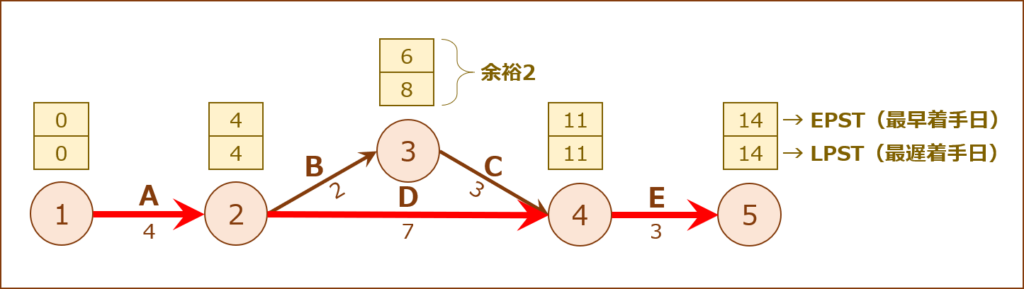
クリティカルパスを特定する。
開始から完了までの複数の経路の中で、最長の経路を「クリティカルパス」といいます。
「クリティカルパス」は「EPST(最早着手日)」と「LPST(最遅着手日)」の差が無いノード(余裕0日)を結合して構成されます。
最短プロジェクト遂行期間の達成に必要な最小費用の算出
今回の問題では、最短プロジェクト遂行期間の達成に必要な最小費用を算出することを求められています。
クリティカルパスである「①→A→②→D→④→E→⑤」の合計作業期間が最短プロジェクト遂行期間となるため、「作業A」「作業D」「作業E」については最短所要期間まで作業を短縮しなければなりませんが、クリティカルパス経路上にない「②→B→③→C→④」については作業期間の余裕があるため、「作業B」「作業C」については最短所要期間まで短縮しなくても最短プロジェクト遂行期間を達成できることが分かります。
「作業B」の作業期間を短縮するには単位時間当たり「50万円」の費用がかかりますが、「作業C」の作業時間を短縮するには単位時間当たり「90万円」の費用がかかってしまうため、「作業B」よりも「作業C」の作業期間を短縮する方が費用がかかってしまうことが分かります。
したがって、「作業C」については、無理に最短所要期間まで短縮するのではなく「最短所要期間+余裕期間 = 3+2 = 5」まで短縮することができれば、最短プロジェクト遂行期間を達成でき、かつ発生する短縮費用を少なく抑えることができます。
これを「アローダイヤグラム」に当てはめてみると、「②→B→③→C→④」の余裕期間が「0」となっていること、かつ最短プロジェクト遂行期間を達成できることが分かります。
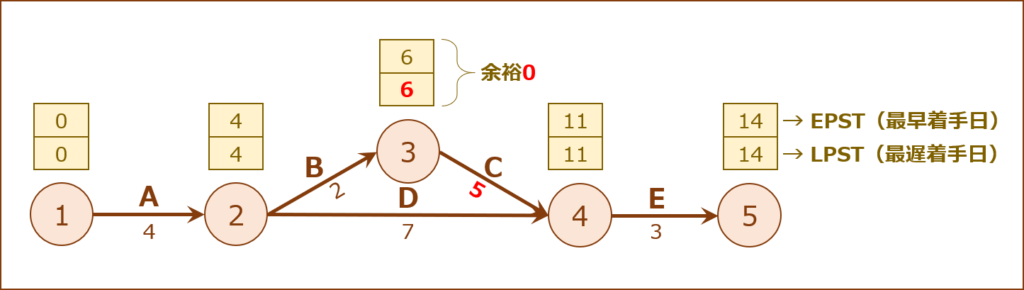
この場合にかかる短縮費用を算出すると以下の通りです。
| 作業名 | 所要期間 | 最短プロジェクト遂行期間を達成するための所要期間 | 必要な短縮期間 | 単位時間当たりの短縮費用(万円) | 最短プロジェクト遂行期間の達成に必要な短縮費用(万円) |
| A | 5 | 4 | 1 | 10 | 10 |
| B | 6 | 2 | 4 | 50 | 200 |
| C | 7 | 5 | 2 | 90 | 180 |
| D | 9 | 7 | 2 | 30 | 60 |
| E | 5 | 3 | 2 | 40 | 80 |
| 合計 | 530 | ||||
答えは(ウ)です。

コメント