今回は、「運営管理 ~R2-16 IE/作業研究(19)連合作業分析~」について説明します。
目次
運営管理 ~令和2年度一次試験問題一覧~
令和2年度の試験問題に関する解説は、以下のページを参照してください。
IE(Industrial Engineering:経営工学)
「IE」は「経営工学」と呼ばれ、生産性を向上させる技術として発展してきました。
その中で、工場の生産活動を対象とした改善の技術は「作業研究」と呼ばれ、工程や動作を分析して改善する「方法研究」と稼動状況や標準時間の設定を研究する「作業測定」で構成されています。
インダストリアルエンジニアリング、経営工学
経営目的を定め、それを実現するために、環境(社会環境及び自然環境)との調和を図りながら、人、物(機械、設備、原材料、補助材料及びエネルギー)、金及び情報を最適に設計し、運用し、統制する工学的な技術・技法の体系。(JISZ8141-1103)
方法研究
「方法研究」は、さらに「工程の分析を行う工程分析」と「作業の分析を行う動作研究」に分類されます。
「工程分析」とは、効率化のために工程を記号で把握して分析することであり、「動作研究」とは、作業の無駄を無くすために動作を分解して分析することです。
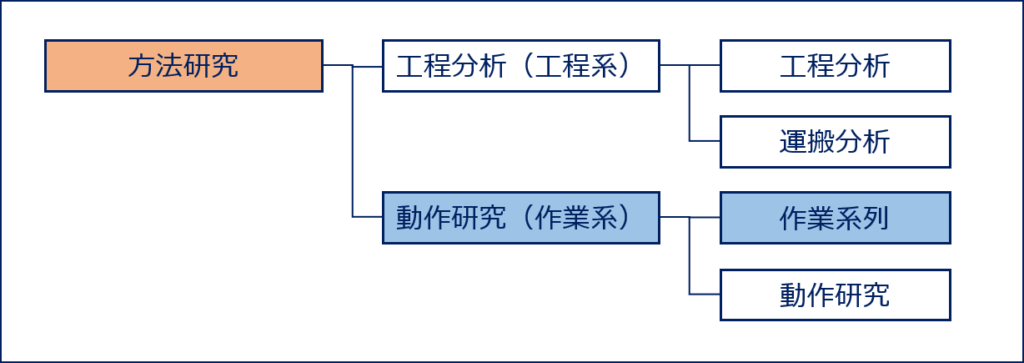
今回は、「IE(作業研究)」「方法研究」「動作研究」「作業系列」に分類される「連合作業分析」について説明します。
連合作業分析
「連合作業分析」とは、作業者や機械による作業を効率化するために、時間の経過に合わせた作業内容の関連性を「ECRSの原則」に従って分析することによって、作業サイクルの時間短縮、作業者や機械の稼働率向上、配置人員数の削減を実現することを目的としています。
「連合作業分析」は、人が機械を使って行う作業内容の関連性を分析する「人・機械分析」と、複数の作業者が協同して行う作業内容の関連性を分析する「組作業分析」に大別されます。
ECRSの原則(改善の4原則)
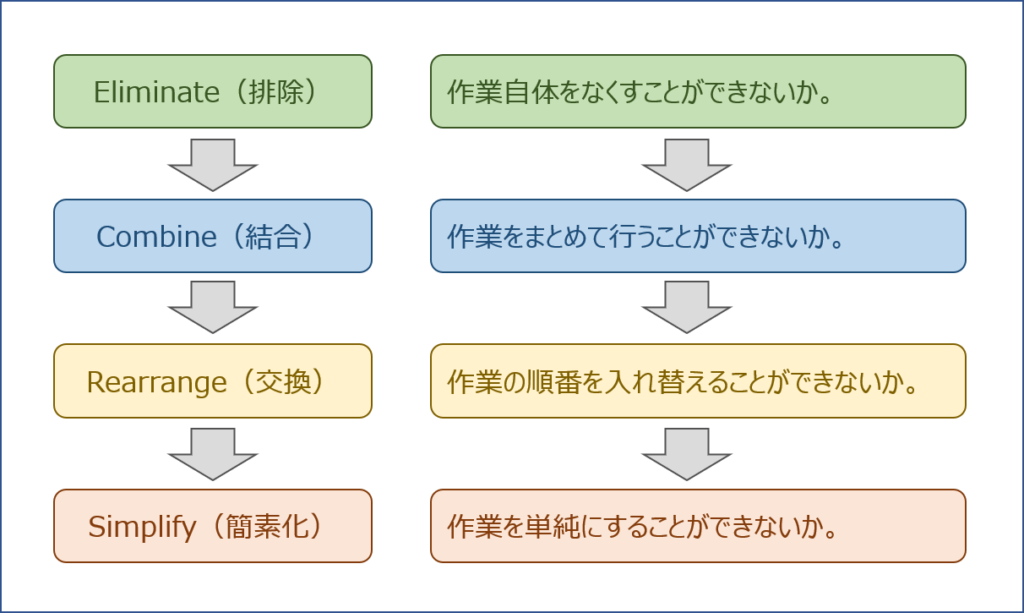
「ECRSの原則」は、生産活動の作業効率を改善するために検討すべき観点とその順番を示しており、Eliminate(排除)、Combine(結合)、Rearrange(交換)、Simplify(簡素化)という4つの観点の頭文字から構成されています。
「ECRSの原則」を活用して、作業自体をなくしたり(E)、作業をまとめて行ったり(C)、作業の順番を入れ替えたり(R)、作業を単純化する(S)といった方法で、生産活動における作業効率を改善していきます。
人・機械分析
「人・機械分析」では、「機械が作業している間の作業者の手待ち」や「作業者が作業している間の機械の停止・空転」といったポイントに着目して改善することによって、作業の効率化を図っていきます。
「人・機械分析」では、作業者が機械を使って行う作業内容を時系列で整理した「マン・マシンチャート」を作成して、作業者と機械の稼動状況に関する問題点を分析します。
マン・マシンチャートの例
例として、平成30年度の事例Ⅲの問題において与えられた「マン・マシンチャート」を以下に示します。作業者と成形機(2台)の稼働状況を時系列で整理することで、作業者と設備の待ち時間が多く稼働率が低い状況となっていることが一目で分かります。
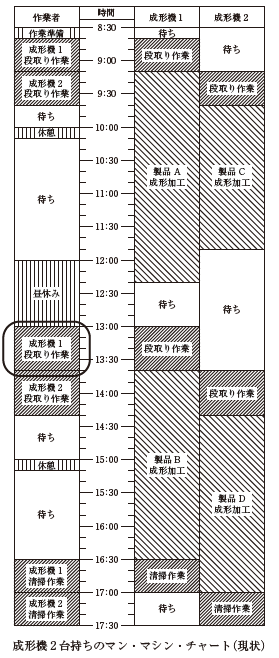
引用元 中小企業診断士試験 平成30年度 事例Ⅲ問題 より
組作業分析
複数の作業者が協同して行う作業を「組作業」といいます。
「組作業分析」では、複数の作業者で実施している「組作業」における作業者相互の稼働関係を記録した結果から、作業方法や人員配置の見直しを行い、作業者が受け持つ作業量の不均衡や手待ちの是正を行うことによって、作業の効率化を図っていきます。
連合作業分析
人と機械、二人以上の人が協同して作業を行う時、その共同作業の効率を高めるための分析手法。(JISZ8141-5213)
試験問題
それでは、実際の試験問題を解いてみます。
【令和2年度 第16問】
ある製品の梱包工程の作業内容は下表に示すとおりである。
この工程を3名の作業者で分担して作業を行う案として、単位時間当たりの生産量が最も多いものを下記の解答群から選べ。
ただし、各作業者間の移動・搬送の時間は無視でき、スペースの制約は考えない。
作業名 作業内容 優先作業 作業時間
(DM)A 箱を組み立てる - 10 B 品物にシールを貼る - 10 C 箱に品物を入れる A,B 30 D 箱に緩衝材を入れる C 15 E 箱のふたをテープでとめる D 10 F 箱にバンドを3本かける E 50 G 製品置場に箱を運ぶ F 25 合計 150
[解答群]
ア 作業者①がA・B・C・D、作業者②がE・F、作業者③がGを担当する。
イ 作業者①がA・B・C・Dを担当し、作業者②がEを実施したのち、作業者②と③が組作業によってFを実施(作業時間が25DMになる)したのち、作業者③がGを担当する。
ウ 作業者①がB・C・D、作業者②がE・F、作業者③がA・Gを担当する。ただし、あらかじめいくつかの箱を組み立てておく。
エ 作業者①がC・D・E、作業者②がF、作業者③がA・B・Gを担当する。ただし、あらかじめいくつかの箱を組み立てて、品物にシールを貼っておく。
中小企業診断協会Webサイト(https://www.j-smeca.jp/contents/010_c_/shikenmondai.html)
考え方と解答
「IE(作業研究)」の分析手法である「連合作業分析」に関する知識を問う問題です。
「連合作業分析」とは、作業者や機械による作業を効率化するために、時間の経過に合わせた作業内容の関連性を「ECRSの原則」に従って分析することによって、作業サイクルの時間短縮、作業者や機械の稼働率向上、配置人員数の削減を実現することを目的としています。
「連合作業分析」は、人が機械を使って行う作業内容の関連性を分析する「人・機械分析」と、複数の作業者が協同して行う作業内容の関連性を分析する「組作業分析」に大別されます。
今回の問題では、「組作業分析」により、総作業時間の短縮を図ること目的としています。
「組作業分析」では、複数の作業者で実施している「組作業」における作業者相互の稼働関係を記録した結果から、作業方法や人員配置の見直しを行い、作業者が受け持つ作業量の不均衡や手待ちの是正を行うことによって、作業の効率化を図っていきます。
今回の問題では、「単位時間当たりの生産量が最も多いもの」を求められていることを意識しておかないと、誤った答えを選択することになるので、注意が必要です。
正解の求め方
それぞれの選択肢に記述されている内容に基づき「A~G」までの作業を「作業者①~作業者③」に割り振った場合の「作業時間」を算出します。(以下表の左側)
その後、作業時間が一番長い作業者の作業時間を比較して、一番作業時間が短い「選択肢(エ)」が正解ということになります。(以下表の右側)
| 選択肢 | 作業時間(DM) | 作業時間が一番長い 作業者と作業時間(DM) |
||||
| 作業者① | 作業者② | 作業者③ | 合計 | |||
| ア | 65 | 60 | 25 | 150 | 作業者① | 65 |
| イ | 65 | 35 | 50 | 150 | 作業者① | 65 |
| ウ | 55 | 60 | 35 | 150 | 作業者② | 60 |
| エ | 55 | 50 | 45 | 150 | 作業者① | 55 |
なんで?という感じがしますが、なぜそうなるのかを確認していきます。
錯覚してしまう
今回の問題は非常にうまく作られており、以下のような錯覚をしてしまいがちです。
特に「選択肢(イ)」は「箱にバンドを3本かける」作業を作業者2人で組作業として本当に作業時間が半分になるのか?と不思議に思いながらも、実現できるのであれば生産性を向上できそうな気がしてしまいます。
- 一番作業時間が長い「作業F」を「作業者②」と「作業者③」による組作業とすれば、梱包工程に要する製品1個当たりの作業時間が一番短くなるから「選択肢(イ)」が正解なのでは?
- 「作業A」と「作業B」は並行して作業ができるから「作業者③」と「作業者①」に作業を分散すれば梱包工程に要する作業時間が短くなるから「選択肢(ウ)」が正解なのでは?
なお、「選択肢(ウ)」と「選択肢(エ)」に記述されている以下の内容は、正解を求めるためには関係ありません。
- 選択肢(ウ)
ただし、あらかじめいくつかの箱を組み立てておく。 - 選択肢(エ)
ただし、あらかじめいくつかの箱を組み立てて、品物にシールを貼っておく。
1製品に対して梱包工程の作業を実施した場合(間違った考え方)
それぞれの選択肢に記述されている内容に基づき「A~G」までの作業を「作業者①~作業者③」に割り振った場合の「1製品に対して梱包工程の作業を実施した場合に要する作業時間」を図に示すと以下の通りです。
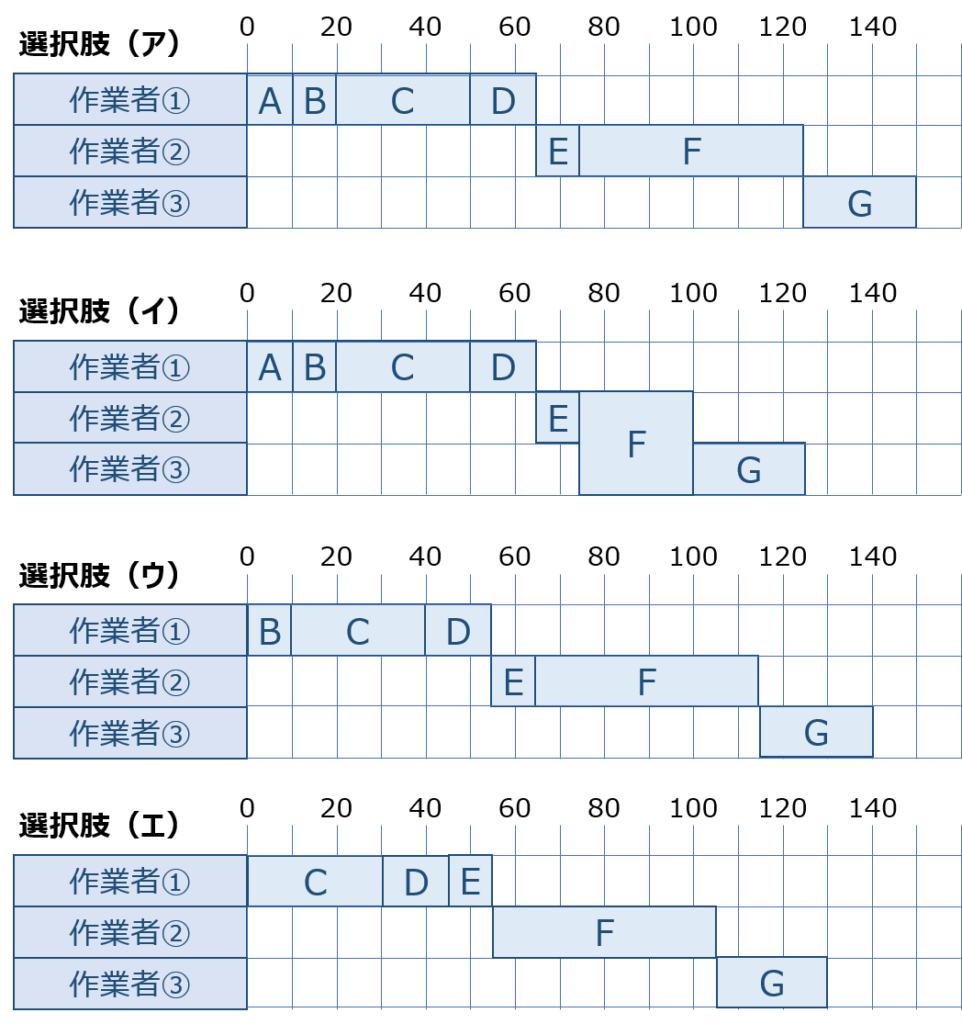
「選択肢(イ)」の場合「125DM」で梱包工程の作業が完了するため、単位時間当たりの生産量が最も多いように感じてしまいますが、この考え方は正しくありません。
連続して梱包工程の作業を実施した場合(正しい考え方)
それぞれの選択肢に記述されている内容に基づき「A~G」までの作業を「作業者①~作業者③」に割り振った場合の「連続して梱包工程の作業を実施した場合に要する作業時間」を図に示すと以下の通りです。
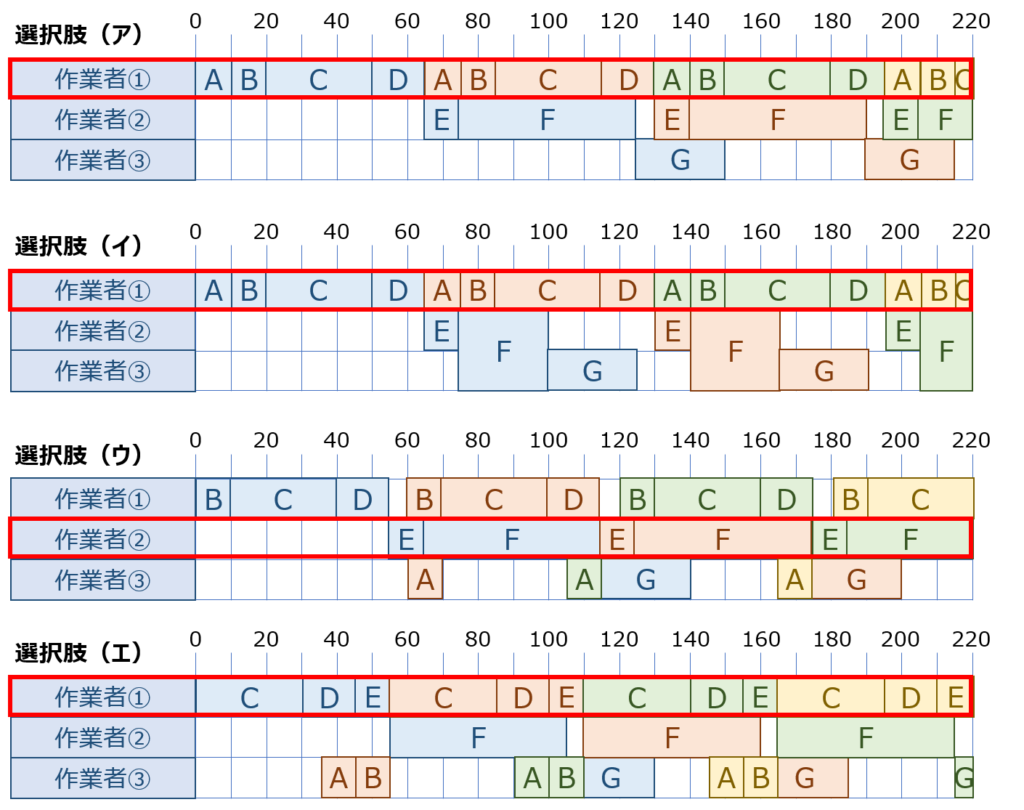
これを見ると、2個目の製品に対する梱包工程の作業が一番早く完了しています。
3個目、4個目の製品に対して作業を実施した場合の図を描いてみれば、さらに分かりやすいと思いますが、これは「単位時間当たりの生産量が最も多いもの」が「選択肢(エ)」であるということを示しています。
なぜ、「選択肢(エ)」が「単位時間当たりの生産量が最も多いもの」になるのか?という疑問に対する答えは、赤枠で囲っている「作業時間が一番長い作業者の作業時間」が一番短くなっているからというのが理由となります。
「選択肢(イ)」の場合「1製品に対して梱包工程の作業を実施した場合に要する作業時間」が「125DM」であったため、単位時間当たりの生産量が最も多いように感じてしまいましたが、作業時間が一番長い「作業者①」の作業時間が短縮されていないため、連続して梱包工程の作業を実施すると、単位時間当たりの生産量は変わっていなかったということです。
今回の問題は、「ライン生産」の「ラインバランシング」に関する問題と考えてよいと思います。時間がある方は、以下のページも併せて確認してみてください。
- 運営管理 ~H28-6 ライン生産(1)工程編成~
- 運営管理 ~H28-21 ライン生産(2)ライン生産~
- 運営管理 ~R1-5 ライン生産(3)ライン生産~
- 運営管理 ~R3-5 ライン生産(4)ライン編成効率~
答えは(エ)です。

コメント