今回は、「財務・会計 ~R1-16 貨幣の時間価値(3)~」について説明します。
二次試験の事例Ⅳで直接出題される論点ではありませんが、「時間価値(現在価値)」は当然に必要な知識として理解しておく必要があるため、一次試験の段階からしっかりと勉強しておきましょう。
目次
財務・会計 ~令和元年度一次試験問題一覧~
令和元年度の試験問題に関する解説は、以下のページを参照してください。
時間価値 -リンク-
一次試験に向けて「時間価値」について説明しているページを以下に示しますのでアクセスしてみてください。
貨幣の時間価値
社債の時間価値
割引現在価値
例えば、100万円の現金を10%の利息が付く銀行に預けると1年後には110万円になります。
つまり、10%の利息が付くことを前提に考えれば、1年後の110万円は、現時点の100万円と同じ価値であると考えることができます。
この場合、現時点での貨幣の価値(100万円)を「現在価値」、1年後の貨幣の価値(110万円)を「将来価値」といい、利息(10%)を「割引率」といいます。
ちなみに、100万円の現金を10%の利息が付く銀行に5年間預けると以下のようになります。

逆に、「将来価値」から「現在価値」を求める場合は以下のようになります。
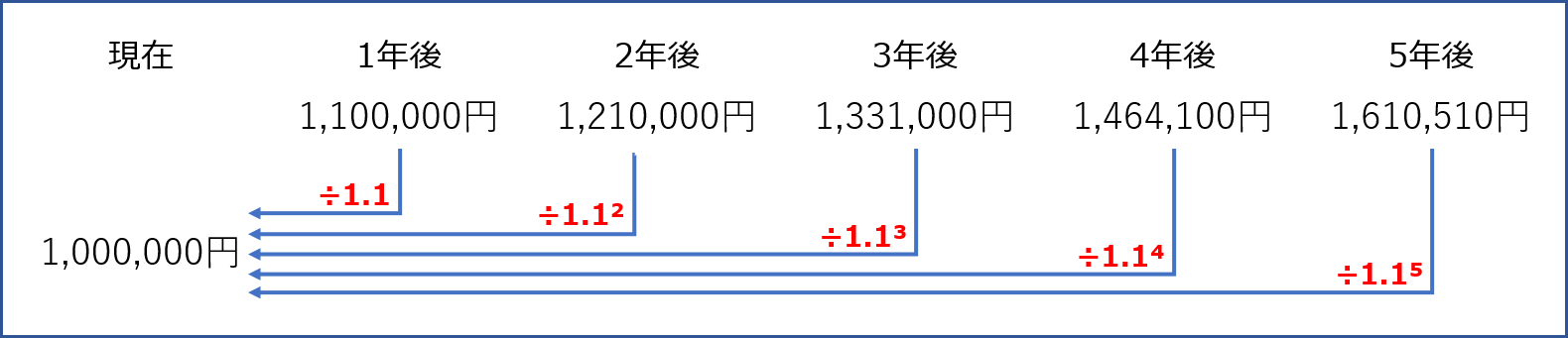
上記のように、「将来価値」を「割引率」で割り引いて求めた「現在価値」のことを「割引現在価値」といいます。
[例題1]
割引率が10%とした場合、5年後に手に入る「1,610,510円」の割引現在価値を求めよ。
[解答]
割引現在価値 = 1,610,510円÷1.1÷1.1÷1.1÷1.1÷1.1 = 1,000,000円
複利現価係数
「複利現価係数」とは「将来価値」から「現在価値」を求めるための係数です。
![]()
「複利現価係数」は、以下の計算式により算出することができます。

「割引率」が「10%」の場合の「複利現価係数」は以下の通りです。
- 1年:1÷1.1 = 0.9090…
- 2年:1÷1.1² = 0.8264…
- 3年:1÷1.1³ = 0.7513…
- 4年:1÷1.1⁴ = 0.6830…
- 5年:1÷1.1⁵ = 0.6209…
[例題2]
割引率が10%とした場合、複利現価係数を用いて5年後に手に入る「1,610,510円」の割引現在価値を求めよ。
| 1年後 | 2年後 | 3年後 | 4年後 | 5年後 | |
| 複利現価係数 | 0.9091 | 0.8264 | 0.7513 | 0.6830 | 0.6209 |
[解答]
割引現在価値 = 1,610,510円 × 0.6209 ≒ 999,966円(四捨五入)
(※)[例題1]と同じ金額を使った問題ですが、複利現価係数の小数点以下第5位以下が切り捨てられているので100万円にはなりません。
年金現価係数
「年金現価係数」とは、今後継続して一定の収入(支出)がある場合の収入総額(支出総額)の割引現在価値を求める係数です。

「割引率」が「10%」の場合の「年金現価係数」は以下の通りです。
- 1年:(1÷1.1) = 0.9090…
- 2年:(1÷1.1)+(1÷1.1²)= 1.7355…
- 3年:(1÷1.1)+(1÷1.1²)+(1÷1.1³)= 2.4868…
- 4年:(1÷1.1)+(1÷1.1²)+(1÷1.1³)+(1÷1.1⁴)= 3.1698…
- 5年:(1÷1.1)+(1÷1.1²)+(1÷1.1³)+(1÷1.1⁴)+(1÷1.1⁵)= 3.7907…
[例題3]
割引率が10%とした場合、今後5年間継続して「1,000,000円」を入手した場合の総収入額の割引現在価値を求めよ。
| 1年後 | 2年後 | 3年後 | 4年後 | 5年後 | |
| 年金現価係数 | 0.9091 | 1.7355 | 2.4868 | 3.1698 | 3.7907 |
[解答]
割引現在価値 = 1,000,000円 × 3.7907 = 3,790,700円
複利現価係数と年金現価係数を用いた割引現在価値の計算
[例題4]
1年後から3年後まで、毎年100万円ずつ収入が入る予定である。
割引率を3%とした場合、複利現価係数と年金現価係数を用いて総収入額の割引現在価値を求めよ。
【今後の収入予定】
| 1年後 | 2年後 | 3年後 | |
| 収入 | ¥1,000,000 | ¥1,000,000 | ¥1,000,000 |
【割引率を3%とした場合の複利現価係数と年金現価係数】
| 1年後 | 2年後 | 3年後 | |
| 複利現価係数 | 0.9709 | 0.9426 | 0.9151 |
| 年金現価係数 | 0.9709 | 1.9135 | 2.8286 |
[解答]
- 複利現価係数を利用した場合の算出方法
1,000,000円 × 0.9709 + 1,000,000円 × 0.9426 + 1,000,000円 × 0.9151 = 2,828,600円 - 年金現価係数を利用した場合の算出方法
1,000,000円 × 2.8286 = 2,828,600円
年金現価係数を用いた割引現在価値の計算
たまにパズルのような問題が出題されることもあります。
[例題5]
割引率が10%とした場合、年金現価係数を用いて5年後に手に入る「1,610,510円」の割引現在価値を求めよ。
| 1年後 | 2年後 | 3年後 | 4年後 | 5年後 | |
| 年金現価係数 | 0.9091 | 1.7355 | 2.4868 | 3.1698 | 3.7907 |
[解答]
割引現在価値 = 1,610,510円 × 3.7907 - 1,610,510円 × 3.1698 ≒ 999,966円
「貨幣の時間価値」は「設備投資の経済性計算」を解くにあたって、基本中の基本です。
「複利現価係数」と「年金現価係数」が与えられた場合は、その数値を用いて「割引現在価値」を計算しますが、「複利現価係数」と「年金現価係数」が与えられなかった場合は、電卓で「\1,000,000 ÷ 1.1 ÷ 1.1・・・」と計算していかなければなりません。
試験問題
それでは、実際の試験問題を解いてみます。
【令和元年度 第16問】
A社は新社屋の完成に当たって、20年間の火災保険契約を保険会社と結ぶことにした。保険会社によって、(1)保険料300万円を一括して支払う「一括払」タイプ、(2)20回払いで、契約時に20万円、それ以降は年末に20万円ずつ支払う「分割払」タイプの2種類から選ぶことができる。契約時点は年初であり、支払額以外の契約条件は同一である。
この保険契約でA社が選ぶべき支払額のタイプおよびその現在価値の組み合わせとして、最も適切なものはどれか。なお、割引率は5%とし、そのときの年金現価係数は、19年の場合には12、20年の場合には12.5を用いること。
ア 「一括払」:300万円
イ 「分割払」:250万円
ウ 「分割払」:260万円
エ 「分割払」:400万円
中小企業診断協会Webサイト(https://www.j-smeca.jp/contents/010_c_/shikenmondai.html)
考え方と解答
火災保険契約で支払う保険料総額の「割引現在価値」を算出して、A社にとって最適な支払方法を選択する問題です。
「貨幣の時間価値」の算出方法を正確に理解していないと、「分割払」タイプでは「20回に分割して支払う」という条件だけを見て、20年の年金現価係数を用いて「現在価値」を算出するというミスをする可能性があります。
「一括払」タイプの場合、契約時(現時点)に保険料300万円を一括で支払うため、割り引く必要はなく「300万円」が支払金額の現在価値です。
「分割払」タイプの場合、契約時(現時点)に支払う20万円も含めて「合計20回」の保険料を支払います。つまり、1年後から毎年20万円の保険料を「合計19回」支払うことになるため、「年金現価係数」は「19年」の数値を使用して、支払金額の「割引現在価値」を算出します。
- 支払金額の「割引現在価値」
20万円 + 20万円 × 12(年金現価係数)= 260万円
したがって、A社が支払う火災保険契約の支払金額の「割引現在価値」は、「分割払」タイプの方が低く、その金額は「260万円」です。
- 一括払:300万円 > 分割払:260万円
答えは(ウ)です。

コメント